Объяснение:
1.Среднее арифметическое 3-x чисел равно 65.К данной группе чисел добавили число 33 Чему теперь равно среднее арифметическое.
1) 65 * 3 = 195 сумма трех чисел
2) 195 + 33 = 228 сумма четырех чисел
3) 228 : 4 = 57 стало среднее арифметическое
2.Упростите выражение:31n-25m-n-15 = 30n - 25m - 15
3.Упростите выражение:26x+20m+2x-14x = 14х + 20m
4.Вычислите среднее арифметическое чисел:8.7;5.2;2.2;9.9
(8,7 + 5,2 + 2,2 + 9,9) : 4 = 26 : 4 = 6,5
5.Найдите область определения функции y=-6x-1
(1-6x) (3x-1)
6.В серии из 10 выстрелов стрелок показал такие результаты:6;9;6;7;9;10;9;9;6
7.Число ДТП за 10 лет на дорогах составляет такой ряд:4450;3890;4720;4640;4390;4580;4060;4530
Найдите разность среднего арифметического и медианы этого набора чисел.
1) (4450 + 3890 + 4720 + 4640 + 4390 + 4580 + 4060 + 4530) : 8 = 35260 : 8 = 4407,5 среднее арифметическое
2) (4640 + 4390) : 2 = 4515 медиана
3) 4515 - 4407,5 = 107.5 разность
8.Найдите область определения функции :y=6x+1
x (5x+2)
9.Решите уравнение:-9a-26=-46-7a
- 9а + 7а = - 46 + 26
-2а = - 20
а = - 20 : (-2)
а = 10
10.Решите уравнение:19-6m=-37+m
-6m - m = - 37 - 19
- 7m = - 56
m = - 56 : (-7)
m = 8
Всего можно составить 24 четырехзначных числа
Из них, на 2 будут делиться 12 чисел, на 4 - 6 чисел, на 11 - 8 чисел.
Объяснение:
Из цифр 2, 4, 7, 9 можно составить 24 четырёхзначных числа, при этом цифры в числах повторяться не будут нам в этом формула перестановок из 4-х элементов:
Р₄=4! =4*3*2*1=24
Сколько же из них будут делиться на 2?
На 2 делятся чётные числа. Среди цифр 2, 4, 7, 9 есть две чётные цифры. Если на месте единиц "закрепить" цифру 2, а остальные три цифры переставлять местами, то получим 3!=3*2*1=6 таких четных чисел. То же повторяем с цифрой 4. Получаем ещё 6 чётных чисел. Всего получено 6+6=12 чисел, делящихся на 2.
На 4 делятся числа, если две его последние цифры нули или образуют число, делящееся на 4. Нулей среди имеющихся у нас цифр нет. Зато из цифр 2, 4, 7, 9 можно составить числа 24, 72 и 92, делящиеся на 4. По очереди "закрепляем" эти цифры в конце числа, а оставшиеся 2 цифры переставляем. Получаем Р₂*3 =2*3=6 чисел делящихся на 4.
Число делится на 11, если сумма цифр, которые стоят на четных местах, равна сумме цифр, стоящих на нечетных местах, либо отличается от неё на 11.
11=2+9, 11=4+7
Числа 2 и 9 ставим на четные места, 4 и 7 - на нечётные места и наоборот, получаем 2*2*2=8 чисел:
2497, 2794, 9427, 9742, 4279, 4972, 7249, 7942
Итак, 8 чисел будут делиться на 11.
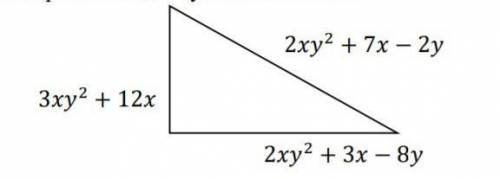
периметр = 2xy² + 7x - 2y + 3xy² + 12x + 2xy² + 3x - 8y = 7xy² + 22x - 10y. Степень многочлена – 2.