Объяснение:
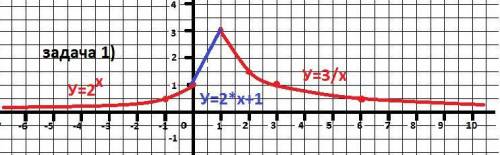
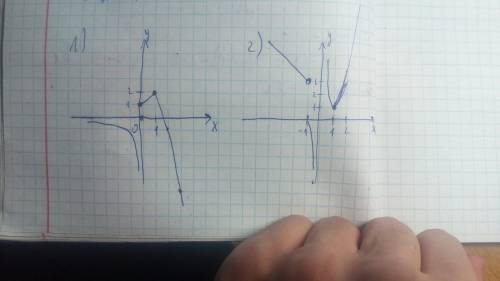
Задача 1) - рисунок к задаче в приложении.
При х=0 обе первых части графика совпадают в точке (0;1)
А третья функция: у = 3/х при х=1 равна
у(3) = 3/3 = 1.
Задача сводится провести прямую через две точки А(0;1) и В(1;3)
ДАНО: А(0;1), В(1;3)
НАЙТИ: Y = k*x + b
РЕШЕНИЕ
1) k = ΔY/ΔX = (Аy-Вy)/(Аx-Вx)=(1-(3))/(0-(1))=2 - коэффициент наклона прямой
2) b=Аy-k*Аx=1-(2)*0= 1- сдвиг по оси ОУ
Уравнение Y(АВ) = 2*x+1 - функция на втором участке.
ОТВЕТ: а = 2 - коэффициент.
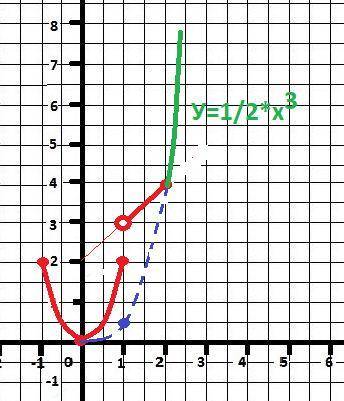
Задача 2) - рисунок в приложении.
При х = 2 на втором участке у = х + 2 = 4.
Задача сводится найти решение
y(2) = a*x³ = a*2³ = a*8 = 4
a = 4/8 = 0.5 = а - коэффициент - ответ.
1) для того чтобы функция была непрерывной, нужно чтобы пределы слева и справа в точках 0 и 1 были равны. Найдем их:
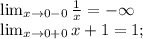
Так как 1≠-∞, то точка 0- это точка разрыва(второго рода).
Чтобы функция была неразрывной в точке 1, нужно чтобы предел от 3-ax^2 был равен 2, так как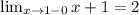 
При x=1 ⇒y=2.
Подставим координаты (1;2) в формулу y=3-ax^2⇒2=3-а⇒а=1, то есть уравнение имеет вид y=3-x^2. Проверим это: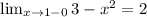 
Действительно 2=2, значит функция не будет являться непрерывной в точке 1.
ответ: х=0 - точка разрыва. функция непрерывна в точке х=1 при а=1
2) Аналогично:
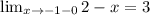
3≠-1, значит -1- это точка разрыва.
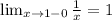
В точке x=1 ⇒y=1. Подставим: 1=a*1⇒a=1.
Проверим: 
.
Так как точка х=0 лежит в области определения функции 
, а из ОДЗ следует что х≠0, то функция также будет прерываться в точке х=0
ответ: х=-1 - точка разрыва, х=0- точка разрыва, функция будет непрерывна в точке х=1 при а=1
№912. а) x^2+3не=0, x-7=0, x=7; б) y^2+1не=0б 3y-1=0, y=1/3;
в) z-1=0, z=1; z+4=0, z=-4; г) 3t+12=0, t=-4; t+2=0, t=-2.
№913. а) 3x^2-3x+x^2-1=0, 4x^2-3x-1=0, x=-0,25; 1;
б) 2y-2-1+2y-y^2=0, -y^2+4y-3=0, y^2-4y+3=0, y=1; 3;
в) 3x-6+x^2-4=0, x^2+3x-10=0, x=-5; 2;
г) y^2-6y+9-12+4y=0, y^2-2y-3=0, y=-1; 3
а) (x+1)^2=4, x+1=2, x=1 или x+1=-2, x=-3
б) (x+2)^2=9, x+2=3, x=1 или x+2=-3, x=-5
в) (x-3)^2=1, x-3=1, x=4 или x-3=-1, x=2
г) (10-x)^2=25, 10-x=5, x=5 или 10-x=-5, x=15