Объяснение:
По определению арифметической прогрессией является последовательность чисел в которой каждый последующий член начиная со второго получается прибавлением к предыдущему некоторого числа
пусть исходная последовательность
a, a+d, a+2d,
что если к каждому члену этой прогрессии прибавить одно и тоже число b, то получится последовательность
a+b, a+d+b, a+2d+b,
a+b, (a+b)+d, (a+b)+d,
получилась последовательность в которой первый член равен a+b а каждый последующий получается прибавлением d что по определению является арифметической прогрессией
За властивістю геом. прогресії кожен член є середнім геометричним двох сусідніх членів:
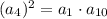
Використаємо формулу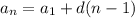 
:
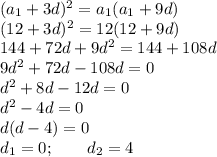
Перший варіант нам підходить. Тоді матимемо стаціонарну арифметична прогресію 12, 12, 12, 12... Стаціонарна арифметична прогресія одночасно є стаціонарною геометричною прогресією.
Другий варіант:
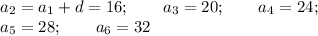
До речі, перевіримо:
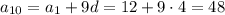
Бачимо, що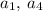 
та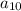 
справді утворюють геометричну прогресію {12; 24; 48} зі знаменником 2.
Відповідь. Умові задовольняють дві прогресії:
1) 12, 12, 12, 12, 12, 12.
2) 12, 16, 20, 24, 28, 32.
Соотношение параметров квадрата
Приведём формулы периметра Р и площади S квадрата через длину стороны а.
периметр квадрата Р равен учетверённому размеру его стороны а: Р = 4 * а;
площадь квадрата S равна квадрату его стороны а: S = a²;
периметр и площадь квадрата связаны между собой. так как в их формулах общий параметр - сторона квадрата: S = P² / 16.
Для понятного объяснения задачи увеличим по заданию его сторону в 3 раза.Тогда новая сторона квадрата станет а1 = 3 * а.
Вычисление увеличения периметра и площади квадрата
Чтобы узнать, как при этом изменились периметр и площадь квадрата, подставим в формулы Р и S вместо "а" новое значение стороны "а1". Тогда:
Р1 = 4 * а1 = 4 * (3 * а ) = 12 * а;
S1 = а1² = (3 * а)² = 9 * а².
После того, как выразили новый периметр Р1 и площадь S1 через начальное значение стороны "а", можно ответить на вопрос задания:
для вычислений используем написанные выше формулы для площади S и периметра P;
чтобы узнать, во сколько раз увеличится периметр квадрата, нужно разделить Р1 на Р;
чтобы узнать, во сколько раз увеличится площадь квадрата, нужно разделить S1 на S.
Согласно выше сказанного, ответим на вопросы задания:
во сколько раз увеличился периметр квадрата, для чего разделим (Р1 : Р) = (12 * а) : (4 * а) = 3 (раза);
во сколько раз увеличится площадь квадрата, для чего разделим (S1 : S) = (9 * а²) : (а²) = 9 (раз).
заметим, что если периметр квадрата увеличился в 3 раза, как и сторона квадрата, то площадь, увеличивается в (3)² = 9 раз.
ответ: периметр увеличится в 3 раза, площадь увеличится в 9 раз.