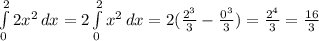
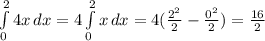
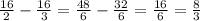
верно , обратное нет
Объяснение:
пусть р - простое , рассмотрим остатки от деления р на 6 :
p = 6b + q , где 0 ≤ q ≤ 5 , если q = 2 , то p = 2(3b+1) , это
число четно и больше 2 , значит не простое , если q = 3 , то
p = 3(2q+1) , это число кратно 3 и больше 3 и значит также не
простое , если q = 4 , то p = 2( 3b + 2) , это число четно и
больше 2 и следовательно не простое , если q = 0 , то p
кратно 6 и не может быть простым , остаются 2 варианта : 1)
q= 1 , то есть p = 6b+1 и 2) q = 5 ⇒ p = 6b + 5 = 6b+6-1 =
6(b+1) - 1 = 6k -1 , а значит любое простое имеет вид : p = 6n±1
обратное утверждение неверно : например число 35 = 6·6 - 1
, но простым число 35 не является
Объяснение:
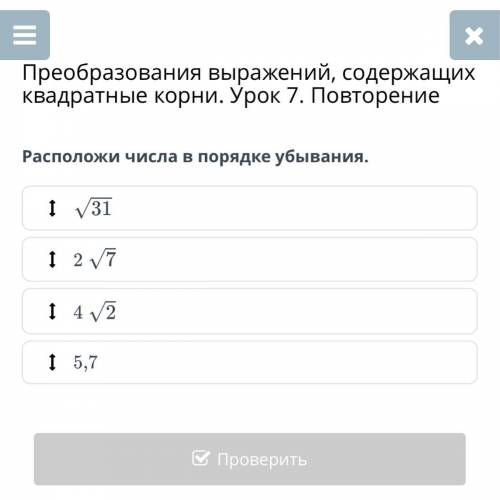
2V7=V(4*7)=V28, 4V2=V(16*2)=V32 (V -корень), 5,7=V32,49
5,7, 4V2, V31, 2V7