а) n-ый член геометрической прогрессии ищется по формуле:
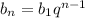
Тогда пятый член этой прогрессии равен:

б) Аналогично по формуле n-го члена геом. прогрессии вычисляем девятый член прогрессии:
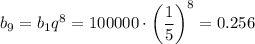
в) Сумма первых n членов геометрической прогрессии ищется по следующей формуле:
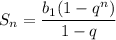
Тогда сумма первых восьми членов этой прогрессии равна:

г) Аналогично с в) по формуле суммы n первых членов геометрической прогрессии вычисляем сумму первых пяти членов этой прогрессии:
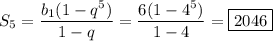
д) Предполагается, что нужно найти сумму бесконечно убывающей геометрической прогрессии:

Тогда
А) -36; - 12; -4;
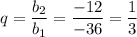
Сумма бесконечно уб. г.п. 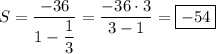
Б) 
Сумма бесконечно убывающей геометрической прогрессии:
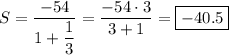
e) используя n-ый член геометрической прогрессии, рассмотрим пятый член этой прогрессии:
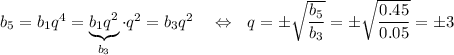
Так как по условию q>0, то q=3
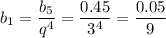
Сумма первых восьми членов этой прогрессии равна:

14х(х-4) - (х+1)(9х-30) 14х²-56х-9х²+30х-9х+30
< 0 < 0
(х+1)(х-4) (х+1)(х-4)
5х²-35х+30 5(х-6)(х-1)
< 0 < 0
(х+1)(х-4) (х+1)(х-4) Нули: -1; 1; 4; 6
+ - + - +
оооо>
-1 1 4 6
ответ: (-1;1)U(4;6)
(х²-25)⁴+(х²+3х-10)²=0
(х-5)⁴(х+5)⁴+(х+5)²(х-2)²=0 Квадратный трехчлен в скобках имеет корни -5 и 2, поэтому его можно разложить на множители (х+5)(х-2)
(х+5)²*( (х-5)⁴(х+5)²+(х-2)² )=0
Первая скобка (х+5)²=0, х=-5
Вторая скобка не может равняться 0, т.к. там записана сумма положительных выражений, а она больше 0.