Алгебра. Найдите сумму корней квадратного уравнения x^2-13x-7=0 Первый По теореме Виета В уравнении вида x²+px+q=0 сумма корней равна х₁+х₂=-р произведение корней равно х₁*х₂=q Отсюда х₁+ х₂=13 Второй не рациональный, верный, но трудоемкий) Дискриминант квадратного уравнения ах²+вх+с=0, определяется по формуле Д=в²-4ас=(-13)²-4*1*(-7)=169+28=197 Корни квадратного уравнения определим по формуле х₁=-в+√Д/2а=13+√197/2*1=13+√197/2 х₂=-в-√Д/2а=13-√197/2*1=13-√197/2
Биквадратное уравнение.
Решается заменой переменной:
Если D >0, т.е.
уравнение имеет корни:
Обратный переход:
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Аналогично
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:
0=1 - неверно, нет таких значений а
Если , т.е
, т.е 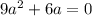
При
уравнение принимает вид:
уравнение не имеет корней
При
уравнение принимает вид:
Уравнение 4-ой степени, значит
О т в е т. При