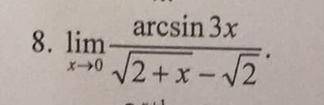
![\lim\limits_{x \to 0}\dfrac{arcsin3x}{\sqrt{2+x}-\sqrt2}=\lim\limits _{x \to 0}\dfrac{arcsin3x\cdot (\sqrt{2+x}+\sqrt2)}{(\sqrt{2+x}-\sqrt2)(\sqrt{2+x}+\sqrt2)}=\\\\\\=\lim\limits _{x \to 0}\dfrac{arcsin3x\cdot (\sqrt{2+x}+\sqrt2)}{2+x-2}=\Big[\ arcsin3x\sim 3x\, ,\ (3x)\to 0\ \Big]=\\\\\\=\lim\limits _{x \to 0}\dfrac{3x\cdot (\sqrt{2+x}+\sqrt2)}{x}=\lim\limits_{x \to 0}3(\sqrt{2+x}+\sqrt2)=3\cdot 2\sqrt2=6\sqrt2](/tpl/images/1462/3670/be35e.png)
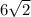 Объяснение:1 Запишем
Объяснение:1 Запишем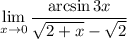 2 Умножим на 1
2 Умножим на 1Но мы представим 1 как дробь 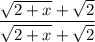 , такое действие еще называют домножением на сопряжённое
, такое действие еще называют домножением на сопряжённое
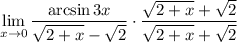
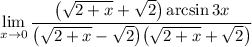
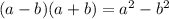 где
где
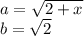
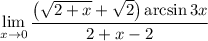
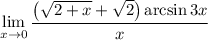
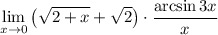 7 Представим предел произведения как произведение пределов
7 Представим предел произведения как произведение пределов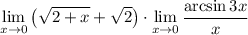 8 Посчитаем первый предел
8 Посчитаем первый предел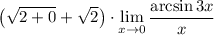
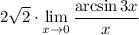 9 Так как
9 Так как 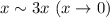 то мы можем заметить в пределе
то мы можем заметить в пределе  на
на 
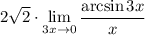 10 Умножим выражение пол пределом на 1
10 Умножим выражение пол пределом на 1Но 1 мы представим в виде 
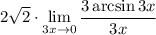
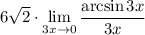
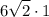 ОТВЕТ
ОТВЕТ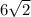
1)sin229° + cos319° + ctg229° * ctg319°=
=sin229°+cos(90°+229°)+ctg(49°+180°)*ctg(139°+180°)
Используя формулу cos(90°+t)=-sint, преобразуем выражение cos(90°+229°)=
=-sin229°
Упростим ctg(49°+180°)=ctg49° и
ctg(139°+180°)=ctg139° ,используя
ctg=(t+k*180°)=ctgt ,где k принадлежит z
В итоге получаем:
sin229°-sin229°+ctg49° * ctg139°=
=ctg49° * ctg139°≈-1
2)( -18cos335°/cos155°*cos60° )-16=
=( -18cos(180°+155°)/cos155°*1/2 )-16=
=( -18cos*(-cos155°)/cos155°*1/2 )-16=
=( -18*-1 / 1*1/2 )-16=( 18/ 1/2 )-16=
=36-16=20