По условию посдедняя цифпа числа х1 не 0 и не 5 (иначе делится на 5), а значит цифра y1 равно либо 1,2,3,4,6,7,8 или 9, тогда последняя цифра числа х2 а значит и число y2 равны либо 2, 4, 6, либо 8
Так как ..2+2=...4;
...4+4=..8
..6+6=...2
...8+8...=6
то последовательность y2, y3,y4, .... является периодичной с периодом 4.
Поэтому для любого n>1 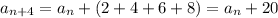
а для любого t>1 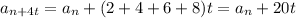
Любое число 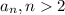 получается имеет вид
получается имеет вид
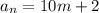 либо
либо 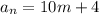 либо
либо 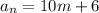 либо
либо 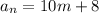 где m -некоторое неотрицательное целое число
где m -некоторое неотрицательное целое число
С двух членов последовательности 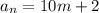 и
и 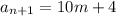 хотя бы одно делится на 4. Запишем его в виде
хотя бы одно делится на 4. Запишем его в виде
a_n=4l
Тогда 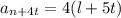
Среди чисел вида l+5t бесконечно много степеней двойки так как остатки от деления на 5 степеней двойки образуют переодическую последовательность 1,2,4,3,1, ... и значит , бесконечно много степеней двойки дают при делении на 5 такой же остаток, как и число l
Встретились
поэт Белов ,
прозаик Чернов ,
пианист Рыжов .
" интересно,у нас белые ,черные и рыжие волосы ,но ни у одного нет волос того цвета на который указывает фамилия",заметил черноволосый
,"ты прав",сказал-Белов .
Следовательно,
Белов может быть только рыжим, поскольку он не беловолосый по условию, и не черноволосый ( с которым он согласился)
Рыжов может быть черноволосым или беловолосым
Чернов может быть беловолосым или рыжеволосым.
Но рыжеволосый уже Белов.
Поэтому Чернов - беловолосый
Рыжов - черноволосый
ответ: Пианист Рыжов черноволосый