Из 12 учеников, выбрать ученика, которому мы дадим первую книгу, можно После этого остается 11 учеников без книг. Из них выбрать следующего ученика, которому мы дадим вторую книгу, можно
Общее число раздать разные (!) книги существует 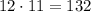 .
.
Другими словами, мы находили размещение из 12 по 2:
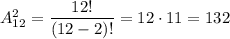
А вот если книги были бы одинаковыми, то порядок выбора учеников был бы не важен: все выбранные ученики получили бы одинаковые книги. В этом случае мы вычисляем сочетание из 12 по 2:
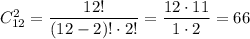
Итак, если учитель раздает разные книги, то существует это сделать. А соответствует случаю, если раздаваемые книги одинаковые.
ответ: 132
Дано уравнение в виде произведения (2sin^2x+3sinx-2)log₇(cosx) = 0.
Приравняем нулю первый множитель с заменой sin x = t.
2t²+ 3 t - 2 = 0. D = 9 + 4*2*2 = 25.
t1 = (-3 + 5)/(2*2) = 1/2,
t2 = (-3 - 5)/(2*2) = -2 (не принимаем по ОДЗ).
Обратная замена: sin x = 1/2.
x = (π/6) + 2πk, k ∈ Z.
x = (5π/6) + 2πk, k ∈ Z.
Рассмотрим второй множитель уравнения: log₇(cosx) = 0.
Он равносилен cos x = 7^0 = 1.
Отсюда х = ( (π/2) + πk, k ∈ Z.
Имеем 3 ответа:
x = (π/6) + 2πk, k ∈ Z.
x = (5π/6) + 2πk, k ∈ Z.
х = ( (π/2) + πk, k ∈ Z.