О т в е т. х=2
Объяснение:Находим производную
y`=(2x2–22x+22)`·e6–x+(2x2–22x+22)·(e6–x)`=
=(4x–22)·e6–x+(2x2–22x+22)·(e6–x)·(6–x)`=
=(4x–22)·e6–x+(2x2–22x+22)·(e6–x)·(–1)=
=e6–x·(4x–22–2x2+22x–22)=
=e6–x·(–2x2+26x–44)
y`=0
–2x2+26x–44=0
x2–13x+22=0
D=132–4·22=169–88=81
x=(13–9)/2=2 или х=(13+9)/2=11
Находим знаки производной.
y`=e6–x·(–2x2+26x–44)
Так как e6–x > 0, знак производной зависит от знака квадратного трехчлена
__–__ (2) __+__ (11)__–_
х=2 – точка минимума, так как производная при переходе через точку меняет знак с – на +
Биквадратное уравнение.
Решается заменой переменной:

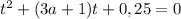
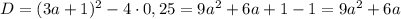
Если D >0, т.е.


уравнение имеет корни:
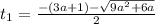 или
или 
Обратный переход:
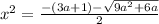 или
или 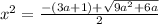
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
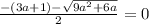
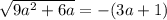
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
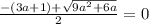
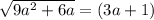
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 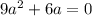
 или
или 
При 
уравнение принимает вид:

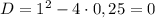 ⇒
⇒ 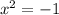
уравнение не имеет корней
При 
уравнение принимает вид:

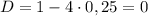 ⇒
⇒ 
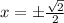
Уравнение 4-ой степени, значит
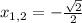 и
и 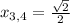
О т в е т. При 
S=Sбічн./8=80:8=10см²