Question

Приведи дроби x2x2−u2 и x−u7x+7u к общему знаменателю. Выбери правильный вариант (варианты) ответа:
1. 7x27(x+u)(x−u) иx2−2xu+u27(x+u)(x−u)

2 7x2x2−u2 иx2−2xu+u2x2−u2

3 7x27(x+u)(x−u) иx2−u27(x+u)(x−u)

4 7x27(x2−u2) иx2−2xu+u27(x2−u2)

5 7x27x2−7u2 иx2−u27x2−7u2

6 другой ответ

7 7x27(x+u)(x−u) иx2−2xu−u27(x+u)(x−u)

Answer 1

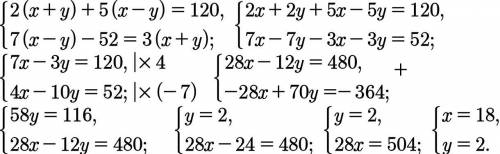
1 и 4.

Объяснение:

x2x2−u2 и x−u7x+7u.

Преобразуем оба знаменателя: первый разложим на множители по формуле сокращённого умножения a2−b2=(a+b)⋅(a−b), во втором вынесем общий множитель 7 за скобки:

x2−u2=(x+u)⋅(x−u);

7x+7u=7⋅(x+u).

Общим знаменателем  (x+u)⋅(x−u)  и  7⋅(x+u) является выражение 7⋅(x+u)⋅(x−u), т. к.

оно делится и на (x+u)⋅(x−u), и на 7⋅(x+u).

Поэтому дробь  x2x2−u2 следует расширить на 7, а дробь x−u7x+7u — на x−u: