При снятии знака модуль получим два варианта,которые и следует рассмотреть:
1) 2Х +5 =\sqrt{2}+\sqrt{3} -3,2
2Х = 1,4+1,7-3,2-5
2Х = -5,1
Х = -2,55
2) -(2Х +5) =\sqrt{2}+\sqrt{3} -3,2
-2Х - 5 = 1,4+1,7-3,2
-2Х = 1,4+1,7-3,2 +5
-2Х = 4,9
Х = -2,45
Відповідь:
1. При каких значениях переменной значение y-6 равняется значению трехчлена y2-9y+3?
9; 1
2. Найдите корни уравнения (2x-1)(2x+1)-x(1-x)=2x(x+1).
то, которое начинается с 3(не -3!!)
3. Найдите дискриминант и количество корней уравнение 2x2-6x-3,5=0.
D = 64
Два корня
4. Найдите периметр прямоугольника, площадь которого равна 70, а одна из сторон на 9 больше другой.
38
5. Найдите корни уравнения x2-8x+20=0.
корней нет
6. При каком значении b имеет один корень уравнение 2x2+4x-b=0.
-2 (не забывайте что писать нужно без пробелов, засчитает за ошибку)
7. При каком значении b имеет один корень уравнение: 3x2-bx+12=0. Если задача имеет несколько решений, то в ответе укажите наибольшее значение b.
12
Пояснення:


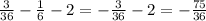
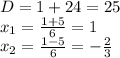
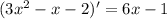

2x+5=sqrt(2)+sqrt(3)-3,2
2x=sqrt(2)+sqrt(3)-8,2
x=(sqrt(2)+sqrt(3))/2-4,1
2x+5>=0 x>=-2,5
(sqrt(2)+sqrt(3))/2-4,1+2.5=(sqrt(2)+sqrt(3))/2-1,6<0 решение не подходит
-2x-5=sqrt(2)+sqrt(3)-3,2
x=-0,9-(sqrt(2)+sqrt(3))/2 x<-2,5 нет решений.
(sqrt(2)+sqrt(3))^2 < 3,2^2
2sqrt(6) < 5,24
sqrt(6) < 2,62
6 < 6,864
ответ нет решений