Круговой турнир по анчурийским шашкам проводится в несколько туров. Все игроки разбиваются на случайные игровые пары. Если
число игроков нечётно, то один случайный игрок остаётся без пары и не участ-
вует в туре. Проигравший в каждой паре (ничья невозможна) выбывает из тур-
нира, а победители и игрок без пары, если он есть, выходят в следующий тур,
который проводится по таким же правилам. Так продолжается до тех пор, пока
не останутся двое. Они играют между собой последнюю партию, которая выяв-
ляет победителя турнира.

👇

Открыть все ответы

Ответ:

ilyaastafiev20

13.10.2021

Для решения рассматриваем три случая, а именно:
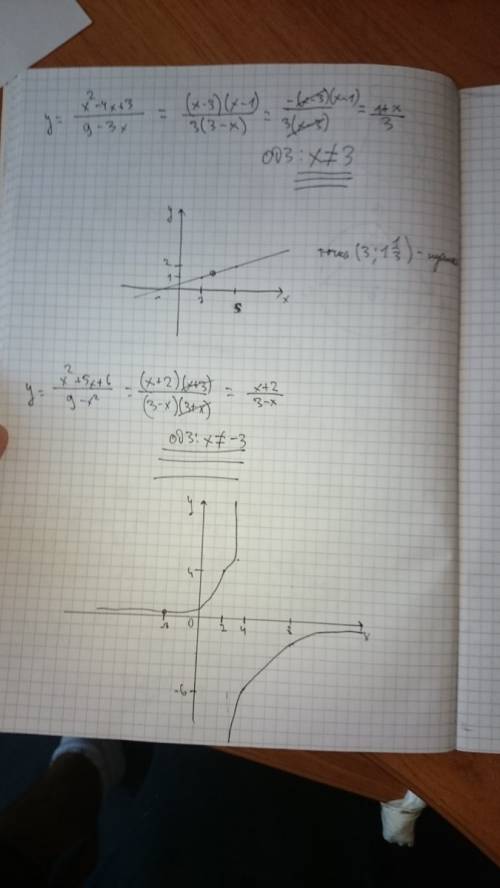
1) трехчлен равен нулю
2) трехчлен меньше нуля
3) трехчлен больше нуля.

Для решения уравнения $x^{2} -7x+6=0$ воспользуемся тем, что сумма все коэффициентов в этом уравнении равна нулю, отсюда следует, что один корень x=1

, а второй равен частному свободного члена на первый: x=6

. Так же можно было решать по теореме Виета: произведение корней равно шести, а их сумма семи.
Итак, x=1

нули этого трехчлена, потому что при них значение этого выражения будет равно нулю.
Теперь, чтобы данное выражение было больше нуля, это будут все решения за нулями, то есть:

и наоборот, чтобы значение выражения было отрицательно нужно брать значения из отрезка между нулями, то есть:

. Все, решено!
ответ:
при x=1

при

4,8(100 оценок)

Ответ:

viktoiabekkknuv

13.10.2021

В первом графике квадратное уравнение
(x^2-4x+3) = 0
имеет корни 3 и 1, поэтому
трехчлен (x^2-4x+3) = (x-3)(x-1)
дробь превращается в выражение вида:
y = (x-3)(x-1)/3(3-x) = -(x-1)/3 поскольку (x-3) и (3-х) в числителе и знаменателе алгебраической дроби сокращаются. Получается функция вида
y = -x/3 + 1/3 а она - линейная и её график - прямая линия. Функция имеет единственный корень при x = 1. В этом месте линия пересекает ось ОХ (абсцисс). При х = 0 у = 1/3. Это значит, что линия пересекает ось ординат (ОУ) при у = 1/3.

Со второй функцией я проврался (неверно определил корни трехчлена числителя), а потому все свои рассуждансы убрал: правильное решение уже дал ProstoD

Построить графики функций а) y=(x^2-4x+3)/(9-3x) б) y=(x^2+5x+6)/(9-x^2) я знаю как выглядит данный