Ты не тупой, просто над алгеброй всегда приходится потеть)
Итак, нам нужно будет составить уравнение, но сначала указываем:
Длина прямоугольника — x, поскольку она нам неизвестна
Ширина прямоугольника — (x-8) см
S прямоугольника — х*(х-8) = (х² - 8х) см
Новая длина прямоугольника — (х+6) см, ширина прямоугольника — (х-8) см
Новая S — (х+6)*(х-8) = х²-2х-48 см
Новая площадь больше старой на 72 см², как говорится в условии задачи. Теперь составляем уравнение:
х²-2х-48-(х²-8х) =72
х²- 2х - 48 - х²+ 8х =72
6х-48 = 72
6х = 120
х = 20 (см) — длина
20-8-12(см) — ширина
P=2(20+12)=2*32=64(см) — P прямоугольника
Если что-то не понял, то спрашивай
Объяснение:
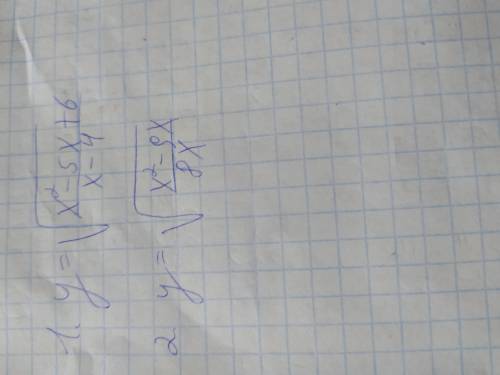
Подкоренное выражение х²-5х+6 /х-4 ≥0 х²-5х+6 ≥ 0 0 ∠ х-4
(х-3)(х-2)≥0
это точки пересечения с осью Х.
Парабола ветвями вверх,
значит она отрицательна между корнями ,если при этом и знаменатель отрицательный,то дробь положительна. х-4∠0 х∠4
2≤ х ≤3 общий ответ 2≤ х ≤3. Теперь рассмотрим случай когда оба положительны и числитель и знаменатель.
4∠х знаменатель положительный. А числитель неотрицательный,когда х находится правее большего и левее меньшего корня.
х≤2 или 3≤х общий ответ 4∠х
ООФ 2≤ х ≤3 или 4∠х
2)Подкоренное выражение х²-9х/8х ≥0 х(х-9) ≥ 0 0 ∠ 8х
х(х-9)≥0 -это точки пересечения с осью Х.
х∠0 или 9 ∠х числитель положителен. знаменатель положителен при 0∠х общим ответом в этой части 9∠х
тепреь рассмотрим ,когда оба отрицательны.
х(х-9)≤0 0≤х≤9
знаменатель меньше нуля при х∠0 . Это должно выполняться одновременно.0∠х≤9 обратите внимание,что х строго больше 0! Поскольку делить на 0 нельзя!
Теперь можем объединить ответы. от 0 до 9 включительно рабортает нижний ответ,а после этого верхний. Значит можно просто записать ООФ : 0∠х