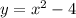
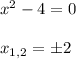
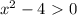
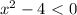
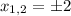, кроме того функция представляет собой параболу. 
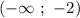- функция принимает положительные значения; в промежутке 
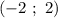отрицательные и в промежутке 
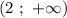— положительные.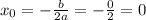
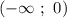и возрастает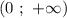 
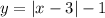
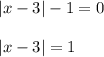
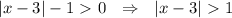
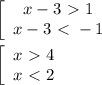
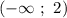- функция принимает положительные значения, в промежутке 
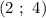— отрицательные и в промежутке 
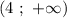— положительные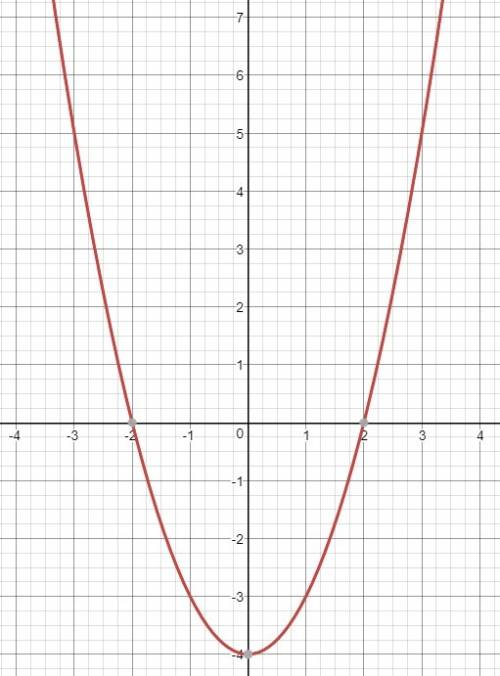
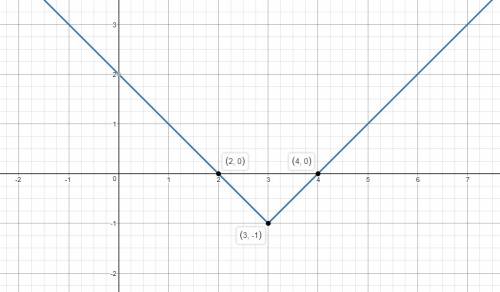
U^2-4+u^3-u+1=u^2-3+u^3-u+1