х - скорость лодки до острова
х+1 - скорость лодки на обратном пути
24/x - время лодки до острова
24/х+1 - время лодки на обратном пути
На путь до острова на 2 часа больше.
24/x - 24/х+1 = 2, общий знаменатель х(х+1), получаем:
24(х+1) - 24*х = 2 х(х+1)
24х + 24 - 24х = 2х² + 2х
24 = 2х² + 2х
-2х² - 2х +24 = 0
2х² + 2х -24 = 0, разделим на 2 для удобства вычислений:
х² + х -12 = 0, квадратное уравнение, ищем корни:
х₁,₂ = (-1 ± √1+48) /2
х₁,₂ = (-1 ± √49) /2
х₁,₂ = (-1 ± 7) /2
х₁ = -4, отбрасываем, как отрицательный
х₂ = 3 (км/час) - скорость лодки до острова
Відповідь:
Пояснення:
2) у=4х^3-2/х = 4x^3 - 2x^(-1)
Використовуємо формулу похідної від степеня: (x^n)' = n * x^(n - 1) і похідної від суми: (u + v)' = u' + v'
y' = (4x^3)' - (2x^(-1))'
Виносимо константу y' = 4(x^3)' - 2(x^(-1))'
y' = 4 * 3 * x^2 - 2 * (-1) * x^(-2) = 12x^2 + 2/(x^2)
3) у=3/х -2√х+7 = 3 * x^(-1) - 2 * x^0,5 + 7
y' = 3 * (x^(-1))' - 2 * (x^0,5)' + 7' = 3 * (-1) * x^(-2) - 2 * 0,5 * x^(0,5 - 1) + 0 =
= -3/x^2 - x^(-0,5) = -3/x^2 + 1/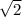
4) у=5sin x-7 cos x
Використовуємо формули похідної від sin x i cos x:
(sin x)' = cos x; (cos x)' = -sin x
y' = 5 * (sin x)' - 7 * (cos x)' = 5cos x + 7sin x
Рассмотрим выражение (y-1)² + 4
(y-1)² - квадрат числа всегда является неотрицательным числом, то есть для любого y выполняется неравенство: (y-1)² ≥ 0
Прибавим 4 и получим, что (y-1)² + 4 ≥ 4
Тогда -((y-1)² + 4) ≤ -4 что всегда меньше 0