y = x³ - 4x²
Найдём производную :
y' = (x³)' - 4(x²)' = 3x² - 8x
Найдём критические точки, для этого приравняем производную к нулю.
y' = 0
3x² - 8x = 0
x(3x - 8) = 0
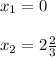
Отметим критические точки на числовой прямой и выясним знаки производной на промежутках, на которые эти точки разбивают числовую прямую .
y'(x) + - +
____________0___________2 2/3_____________
y(x) ↑ ↓ ↑
На промежутках (- ∞ ; 0] и [2 2/3 ; + ∞) -функция возрастает
На промежутке [0 ; 2 2/3] - функция уюывает
а)5х+(7у-х)-(3х+7у)=5х+7у-х-3х-7у=(5х+(-х-3х))+(7у-7у)=1х
б)8(х-3)+4(5-2х)=8х-24+20-8х=(20-24)+(8х-8х)=(-4)
Объяснение:
а)когда за скобках минус ты рассказываешь скобки то знаки меняются в противоположную сторону.