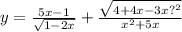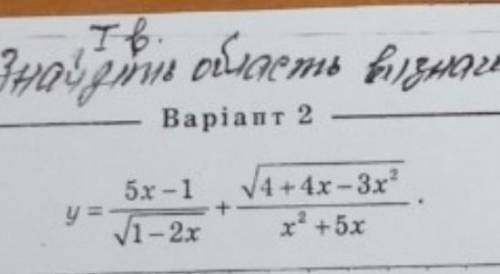
Дано функцію f(x) = (x^2-8x)/(x+1)
Знаходимо найбільше і найменше значення даної функції на проміжку [-5,-2].
f(-5) = ((-5)^2-8*(-5))/(-5+1) = 65/(-4) = -16,25.
f(-2) = ((-2)^2-8*(-2))/(-2+1) = 20/(-1) = -20.
Визначаємо точки екстремуму даної функції.
Знаходимо первісну:
f'(x) = (2x-8)*(x+1) - 1*(x^2-8x))/((x+1)^2) = (x^2 + 2x - 8)/((x + 1)^2).
Прирівнюємо їі до 0 (достатьно чисельник):
x^2 + 2x - 8 = 0, Д = 4+4*8 = 36, х1 = (-2 - 6)/2 = -4, х2 = (-2 + 6)/2 = 2.
Знаходимо знаки первісної:
х = -5 -4 1 2 3
y' = 0,4375 0 -1,25 0 0,4375 .
У точці х = -4 маємо максимум функції,
f(-4) = ((-4)^2-8*(-4))/(-4+1) = 48/(-3) = -16.
Відповідь:
- найбільше значення даної функції на проміжку [-5,-2] дорівнює -16,
- найменше значення даної функції на проміжку [-5,-2] дорівнює -20,
- максимум функції у точці х = -4,
- мінімум функції у точці х = 2.
1) a/16 + x/16 =(a+x)/16
2) 5m/n - 3m/n =2m/n
3) 3x +4y/12 - x+2y/12 =2x+6y/12=2x+y/2
4) a+2b/2c - a-4b/2c =b/c-2b/c=-b/c
5) a-8/a^2-25 + 13/a^2-25 =a-8/(a+5)*(a-5)
6) 5x+1/2 - x/2 =9x/2+1/2=4,5x+1/2
7) a+3/4 - a+1/4 =4/4=1
8) 2x/a-b - x/b-a =2x/a-b + x/a-b=3x/a-b
9) a/x-1 + b/1-x =a/x-1 - b/x-1=a-b/x-1
10) a-5/a-3 + a+5/3-a =a-5/a-3 - a+5/a-3=(a-5)*(a+5)/a-3=(a^2-25)/a-3
11) 3x-2/5 + 5x-3/3 =(9x-6+25x-15)/15=(24x-21)/15=3*(8x-7)/15=(8x-7)/5
12) 2m+5/6 - m-a/8 =m+(20-6a)/24=m+2*(10-3a)/24=m+(10-3a)/12
13) 7/10a -5/4a =(70-25)/20a=45/20a=9/4a
найти область определения/ знайти область визначення 
Объяснение:
D(y):
{-3x^2+4x+4 >=0
{1-2x>=0
{x(x+5)≠0
{-3(x-2)(x+2/3)>=0
{x=<1/2
{[x≠0
{[x≠-5
{-2/3=<x=<2
{x=<1/2
{[x≠0
{[x≠-5
D(y): x∈[-2/3;0)∨(0;1/2]