Зная автора задания как специалиста (в частности) в области геометрии, после первых неудачных попыток сделать эту задачу я подумал о возможности применить геометрию, после чего появилась надежда на успех.
Во-первых, мы можем считать, что x > 0 (если x<0, то y(x)>y(-x), то есть при отрицательном x наименьшее значение достигаться не может. Значение y(0)=6 пока просто запомним).
Пусть x>0 - некоторое число. Рассмотрим два . треугольника, один со сторонами 2 и x и углом в 30° между ними, второй - со сторонами 4 и x и углом в 90° между ними. Совместив их по стороне, равной x, получим 4-хугольник ABCD со сторонами AB=2, BC=4, диагональю BD=x и углом ABC, который диагональ BD делит на углы ABD=30° и DBC=90°. По теореме косинусов
Поэтому y(x) при положительном x - это сумма сторон AD и DС. Меняя x, мы меняем вершину D, двигая ее по лучу с вершиной B (при неподвижных A, B и C). Ясно, что сумма будет минимальной, когда четырехугольник ABCD вырождается (это когда D лежит на AC), и равна стороне AC,
Поскольку ответом в задаче будет
Замечание. Значение в нуле в принципе мы могли не вычислять, считая, что при этом получается вырожденный четырехугольник с нулевой диагональю.
1. (7-4√3) (4+4√3+ 3)= (7-4√3)(7+4√3)= 7^2- (4√3)^2= 49-48=1 В общем, сначала второй пример возвела в квадрат, потом по формуле разность квадратов получила ответ 1. 2. Я не знаю, как можно написать здесь, но попробую. сначала (x-6)(x+6) общий знаменатель. получается в числителе x^2+6x+x^2-6x-x+6-54+5x=0, а знаменатель тот же. В итоге, когда ты найдешь подобные члены, получается выражение 2x^2+4x-48=0; можно сократить на 2, получается x^2+2x-24=0. По теореме Виета получаются корни -6, 4. НО. Есть, так называемое ОДЗ(область допустимых значений). НЕЛЬЗЯ, чтобы у тебя обнулялся знаменатель, иначе получится деление на 0, а на ноль делить нельзя. Получается, что корнями не могут быть 6 и -6, иначе у тебя в знаменателе будет 0. А один из корней получился -6. Значит ответ будет только 4. ответ: 4.
Зная автора задания как специалиста (в частности) в области геометрии, после первых неудачных попыток сделать эту задачу я подумал о возможности применить геометрию, после чего появилась надежда на успех.
Во-первых, мы можем считать, что x > 0 (если x<0, то y(x)>y(-x), то есть при отрицательном x наименьшее значение достигаться не может. Значение y(0)=6 пока просто запомним).
Пусть x>0 - некоторое число. Рассмотрим два . треугольника, один со сторонами 2 и x и углом в 30° между ними, второй - со сторонами 4 и x и углом в 90° между ними. Совместив их по стороне, равной x, получим 4-хугольник ABCD со сторонами AB=2, BC=4, диагональю BD=x и углом ABC, который диагональ BD делит на углы ABD=30° и DBC=90°. По теореме косинусов
Поэтому y(x) при положительном x - это сумма сторон AD и DС. Меняя x, мы меняем вершину D, двигая ее по лучу с вершиной B (при неподвижных A, B и C). Ясно, что сумма будет минимальной, когда четырехугольник ABCD вырождается (это когда D лежит на AC), и равна стороне AC,
Поскольку ответом в задаче будет
ответом в задаче будет 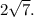
Замечание. Значение в нуле в принципе мы могли не вычислять, считая, что при этом получается вырожденный четырехугольник с нулевой диагональю.