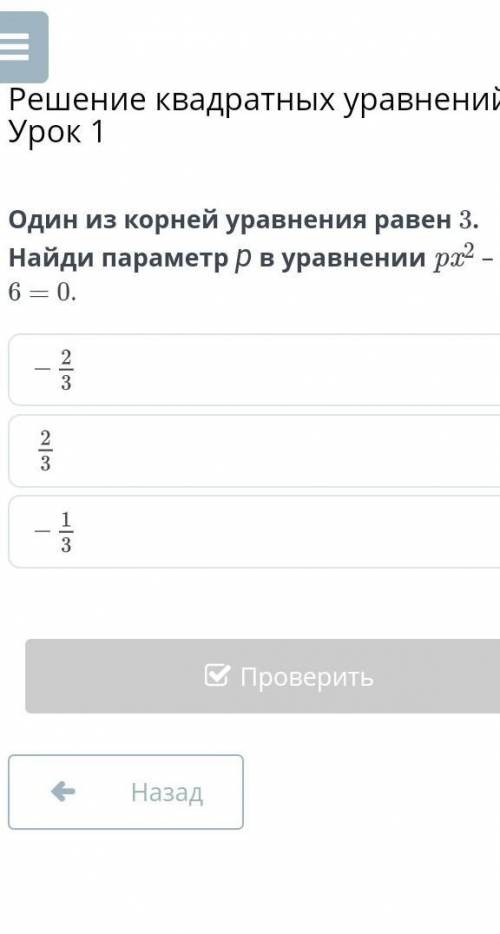
2/3
Объяснение:
Объяснение:
Как найти область определения функции?
Примеры решений
Если где-то нет чего-то, значит, где-то что-то есть
Продолжаем изучение раздела «Функции и графики», и следующая станция нашего путешествия – Область определения функции. Активное обсуждение данного понятия началось в статье о множествах и продолжилось на первом уроке о графиках функций, где я рассмотрел элементарные функции, и, в частности, их области определения. Поэтому чайникам рекомендую начать с азов темы, поскольку я не буду вновь останавливаться на некоторых базовых моментах.
Предполагается, читатель знает область определения следующих функций: линейной, квадратичной, кубической функции, многочленов, экспоненты, синуса, косинуса. Они определены на (множестве всех действительных чисел). За тангенсы, арксинусы, так и быть, прощаю =) – более редкие графики запоминаются далеко не сразу.
Область определения – вроде бы вещь простая, и возникает закономерный вопрос, о чём же будет статья? На данном уроке я рассмотрю распространённые задачи на нахождение области определения функции. Кроме того, мы повторим неравенства с одной переменной, навыки решения которых потребуются и в других задачах высшей математики. Материал, к слову, весь школьный, поэтому будет полезен не только студентам, но и учащимся. Информация, конечно, не претендует на энциклопедичность, но зато здесь не надуманные «мёртвые» примеры, а жареные каштаны, которые взяты из настоящих практических работ.
Начнём с экспресс-вруба в тему. Коротко о главном: речь идёт о функции одной переменной . Её область определения – это множество значений «икс», для которых существуют значения «игреков». Рассмотрим условный пример:
Область определения функции
Область определения данной функции представляет собой объединение промежутков:
(для тех, кто позабыл: – значок объединения). Иными словами, если взять любое значение «икс» из интервала , или из , или из , то для каждого такого «икс» будет существовать значение «игрек».
Грубо говоря, где область определения – там есть график функции. А вот полуинтервал и точка «цэ» не входят в область определения и графика там нет.
Да, кстати, если что-нибудь не понятно из терминологии и/или содержания первых абзацев, таки лучше вернуться к статьям Множества и действия над ними, Графики и свойства элементарных функций.
Как найти область определения функции? Многие помнят детскую считалку: «камень, ножницы, бумага», и в данном случае её можно смело перефразировать: «корень, дробь и логарифм». Таким образом, если вам на жизненном пути встречается дробь, корень или логарифм, то следует сразу же очень и очень насторожиться! Намного реже встречаются тангенс, котангенс, арксинус, арккосинус, и о них мы тоже поговорим. Но сначала зарисовки из жизни муравьёв:
Область определения функции, в которой есть дробь
Предположим, дана функция, содержащая некоторую дробь . Как вы знаете, на ноль делить нельзя: , поэтому те значения «икс», которые обращают знаменатель в ноль – не входят в область определения данной функции.
Не буду останавливаться на самых простых функциях вроде и т.п., поскольку все прекрасно видят точки, которые не входят в их области определения. Рассмотрим более содержательные дроби
ответ:Решение методом подстановки.
1) (-y+5;y), y∈ R
{ x = − y + 5
y = − x + 5
{ x = − y + 5
y = − ( − y + 5 ) + 5
{ x = − y + 5
0 = 0
2) решений нет (прямые параллельны).
{ 2 x + y = 8
10 x + 5 y = 10
{ y = − 2 x + 8
10 x + 5 y = 10
--
{ y = − 2 x+ 8
10 x +
5( − 2x + 8 ) = 10
{ y = − 2 x + 8
30 = 0
3)y=-1/3;x=1 2/3
{ y − x = − 2
y + 2 x = 3
---
{ y = x − 2
y + 2 x = 3
-
{ y = x − 2
( x − 2 ) + 2 x = 3
{ y =x − 2
3 x − 5 = 0
{ y = x − 2
x = 5 /3
{ y = − 1 /3
x = 5 /3
4)y = 4 ; x = − 1.
{ y + x = 3
− y + 2 x + 6 = 0
{ y = − x + 3
−y + 2 x + 6 = 0
{ y = − x + 3
− ( − x + 3 ) + 2 x + 6 = 0
{ y = − x + 3
3 x + 3 = 0
{ y = − x + 3
x = − 1
{ y = 4
x = − 1
ЭТО ВСЁ МЕТОД ПОДСТАНОВКИ!
Объяснение: