1) Бродить по парку и собирать цветы.
2)Приятели сворачивают с дороги и углубляются в лес
3)Противительный
4)Плохо видели лебедей , но замерли от восхищения
5)Из высокой болотной травы он соорудил нечто вроде шалаша , но снег быстро занёс этот шалаш.
6)То тут то там что-то сыплется и шуршит
за то , что ты мне
8)Части сложного предложения связываются только подчинительными союзами
9)Ребята очень устали , но всё-таки доделали работу. Ребята очень устали , поэтому они пошли отдыхать.
10)( Непонятно задание ((()
11)Что бы мне почитать о космосе?
12)Изъяснительный
Объяснение:
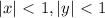
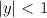возвести в квадрат, получив, 
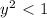, что и требовалось проверить.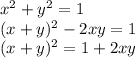
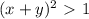
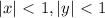, следует, что 0 <x < 1, 0 < y < 1
Решение на фото,.,.,..,.,