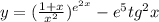
ПРАВИЛЬНО 100%
Объяснение:1)У квадратного уравнения есть три коэффициента:
a = 1.
b = -37.
c = -27.
D = b^2 - 4ac = -37^2 - 4 * 1 * -27 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 38,4318.
x1 = (37 + 38,4318) / (2 * 1) = 37,7159.
x2 = (37 - 38,4318 ) / (2 * 1) = -0,715879.
ответ: 37,7159, -0,715879.
2)У квадратного уравнения есть три коэффициента:
a = 1.
b = -2.
c = -9.
D = b^2 - 4ac = -2^2 - 4 * 1 * -9 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 6,32456.
x1 = (2 + 6,32456) / (2 * 1) = 4,16228.
x2 = (2 - 6,32456 ) / (2 * 1) = -2,16228.
ответ: 4,16228, -2,16228.
3)У квадратного уравнения есть три коэффициента:
a = 2.
b = 7.
c = 6.
D = b^2 - 4ac = 7^2 - 4 * 2 * 6 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 1.
x1 = (-7 + 1) / (2 * 2) = -1,5.
x2 = (-7 - 1 ) / (2 * 2) = -2.
ответ: -1,5, -2.
4)У квадратного уравнения есть три коэффициента:
a = 3.
b = -4.
c = -4.
D = b^2 - 4ac = -4^2 - 4 * 3 * -4 = D > 0, значит у уравнения два вещественных корня (^(1/2) - это знак корня): x = (-b ± D^(1/2))/(2a).
D^(1/2) = 8.
x1 = (4 + 8) / (2 * 3) = 2.
x2 = (4 - 8 ) / (2 * 3) = -0,666667.
ответ: 2, -0,666667.
y = 8x - 3
1. Аргумент = 2, это означает, что х = 2. Подставим это значение в функцию и получим её значение.
y = 8*2 - 3 = 16 - 3 = 13
При х = 2, у = 13
2. Значение функции = -19, это означает, что у = -19. Подставим это значение функции и найдем аргумент:
-19 = 8x - 3
-8х = -3 + 19
-8х = 16 |:(-8)
x = -2
При у = -19, х = -2
3. Чтобы определить, принадлежит ли точка графику функции, необходимо подставить значения её координат в функцию. Если получится верное числовое равенство, то точка принадлежит графику.
В(-2.-13)
-13 = 8 * (-2) - 3
-13 = -16 - 3
-13 = -19 - неверно, поэтому точка В не принадлежит графику функции. В(-2.-13) ∉ y = 8x - 3
Первое слагаемое представляет собой показательно-степенную функцию, для нахождения производной которой необходимо применить логарифмическое дифференцирование. Продифференцируем первое слагаемое отдельно:
Найдем производную заданной функции: