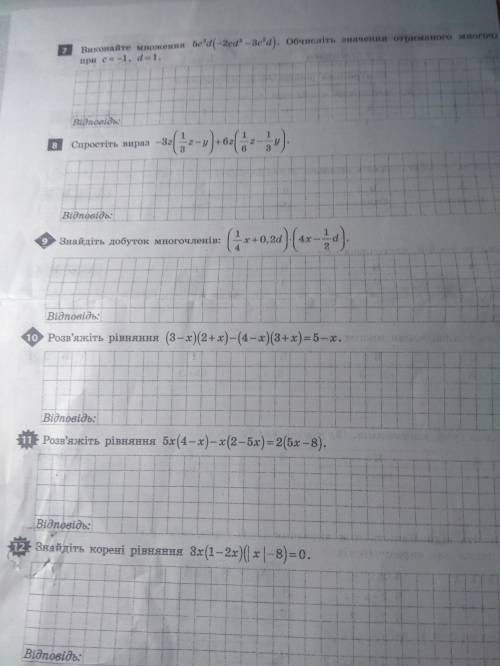
Арифметическая прогрессия - это последовательность чисел, каждый член которой, начиная со 2-го, равен предыдущему, сложенному с одним и тем же числом.
Это число называют разностью арифметической прогрессии и обозначают d.
Значит, а₂ = а₁ + d, a₃ = a₂ + d = а₁ + 2d, ..., an = a₁ + d(n - 1) - формула n-го члена.
Т.к. а₁ = 8, а₇ =26, то используя формулу n-го члена можно записать:
а₇ = а₁ + d(7 - 1), а₇ = а₁ + 6d, 26 = 8 + 6d, откуда 6d = 26 - 8 = 18, т.е. d = 3.
Сумму n первых членов арифметической прогрессии находят по формуле Sn = (a₁ + an)/2 · n или Sn = (2a₁ + d(n - 1))/2 · n.
S₁₀ = (2 · 8 + 3(10 - 1))/2 · 10 = (16 + 3 · 9)/2 · 10 = (16 + 27) · 5 = 43 · 5 = 215.
ответ: 215.
8)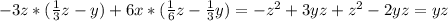
10)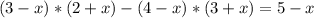
x = 11
11)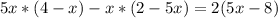
x = -2
12)
x₁ = -8, x₂ = 0, x₃ =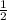 , x₄ = 8
, x₄ = 8