найдите сумму бесконечной геометрической прогрессии -40; 20; -10; ...
член геометрической прогрессии определяется по формуле
вn=в1*q^(n-1),или в2=в1*q^(2-1)= в1*q¹=в1q
т.к. в1=-40; в2=20, по условию задачи, можно найти q, подставляем данные и находим
20=-40*q, q=-½
т.к не дано найти сумму ограниченного количества членов , то можно рассуждать так, суммы n членов определяется по формуле
Sn=в1*(1-q^n)/(1-q), т.к q=-½, тогда q^n=(-½)^n≈0 при n→∞, (-0,5;0,3;-0,25, т.е при увеличении n, q≈0, и этим членом можно пренебречь), тогда, подставив данные получим
Sn=-40*1/(1-(-½))=-40*2/3=-26⅔
-x=x+9/-7x-3 все выражение умножим на (-7x-3), получается
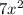 + 3x - x - 9 = 0
+ 3x - x - 9 = 0
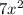 +2x - 9= 0
+2x - 9= 0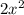 - 4*7*(-9)= 4+252 = 256
- 4*7*(-9)= 4+252 = 256
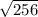 = 16
= 16
-x(-7x-3)=x+9, раскроем скобки
найдем дискриминант:
D=
x1= -2-16/2*7 = -9/7
x2 = -2+16/14 = 1
ответ: 1