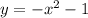
а < 0 ⇒ ветви направлены вниз
-х²-1 ⇒ график функции сдвигается вниз по оси ординат на 1
Подходящий график: Б
2.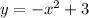
а < 0 ⇒ ветви направлены вниз
-х²+3 ⇒ график функции сдвигается вверх по оси ординат на 3
Подходящий график: Г
3.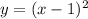
а > 0 ⇒ ветви направлены вверх
(х-1)² ⇒ график функции сдвигается вправо по оси абсцисс на 1
Подходящий график: Д
4.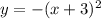
а < 0 ⇒ ветви направлены вниз
(x+3)² ⇒ график функции сдвигается влево по оси абсцисс на 3
Подходящий график: А
5.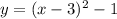
а > 0 ⇒ ветви направлены вверх
(x-3)²-1 ⇒ график функции сдвигается вправо по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: Е
6.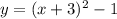
а > 0 ⇒ ветви направлены вверх
(x+3)²-1 ⇒ график функции сдвигается влево по оси абсцисс на 3, да ещё вниз по оси ординат на 1
Подходящий график: В
ответ:1.Правильно
2.Верно
3.Не верно
4.Верно,это третий признак равенства треугольников
5.Не верно
6.Верно
7.Верно
8.Если сторона и прилежащие к ней углы одного треугольника равны стороне и двум прилежащим к ней углам второго треугольника,то такие треугольники равны
9.Нет,не верно,у треугольников могут быть одинаковые углы,но стороны разных размеров
10.Верно,это первый признак равенства треугольников
Объяснение: