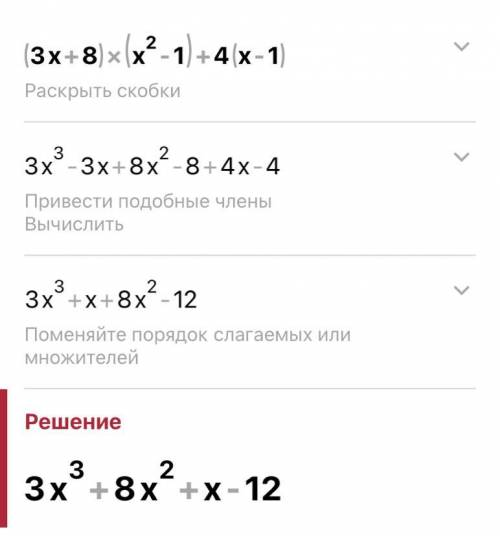
ответ: 24 см и 12 см.
Объяснение:
Пусть l - длина отрезка, соединяющего середины диагоналей трапеции. Этот отрезок лежит на средней линии трапеции и равен полуразности её оснований. Пусть a и b - основания трапеции, причём a>b, а c - длина средней линии трапеции. Так как по условию диагонали трапеции делят её среднюю линию на 3 равных части, то l=c/3. Отсюда c=3*l=3*6=18 см и, так как c=(a+b)/2, то мы получаем систему уравнений:
(a-b)/2=6
(a+b)/2=18
или:
a-b=12
a+b=36
Решая её, находим a=24 см и b=12 см.
∈ 
∞ 
∪ 
∞ 
∞ ∪ ∞ 
∈ 
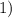
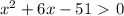
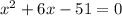
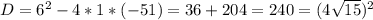
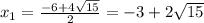
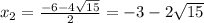
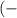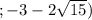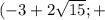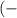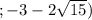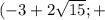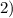
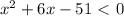
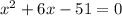
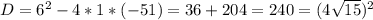
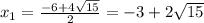
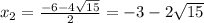
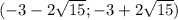
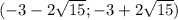
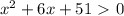
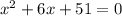
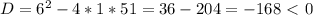
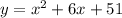
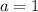положительный, то ветви параболы направлены вверх, а поскольку 
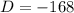отрицательный, то парабола не пересекается с осью 
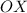. Поэтому парабола 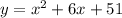расположена над осью 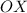; таким образом, при любом значении x имеем y>0. Значит, 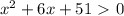при любом значении x. ∞ 
∞ 
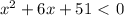
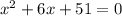
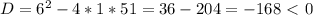
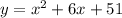
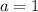положительный, то ветви параболы направлены вверх, а поскольку 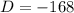отрицательный, то парабола не пересекается с осью 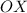. Поэтому парабола 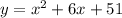расположена над осью 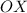; таким образом, при любом значении x имеем y>0. Значит, 
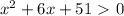при любом значении x. Следовательно, рассматриваемое неравенство не имеет решений. 
