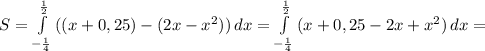
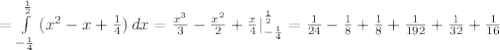
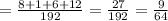Два автобуса выехали одновременно на встречу друг другу из пунктов m и n, расстояние между которыми 70 км, и через 40 мин,одновременно прибыли в промежуточный пункт p. найдите расстояние между пунктами m и p,если известно,что средняя скорость автобуса,выехавшего из пункта m, оказалась на 15 км/ч больше средней скорости автобуса, выехавшего из пункта n.решите ))

👇

Ответ:

Sergay121

27.12.2021

Пусть x км - расстояние между пунктами M и P, тогда (70-х) км - расстояние между пунктами P и N. Зная,что время каждого автобуса равно 40 мин = 2/3 ч ,найдем средние скорости автобусов:

х /2/3=3х/2(км/ч) - средяя скорость 1го автобуса (из пункта M)

(70-х)/2/3=3*(70-х)/2 - средяя скорость 2го автобуса (из пункта N)

Зная,что средняя скорость автобуса,выехавшего из пункта M, оказалась на 15 км/ч больше средней скорости автобуса, выехавшего из пункта N,составим и решим ур-е:

3х/2-3(70-х)/2=15

x-(70-x)=10

x-70+x=10

2x=80

x=40

ответ:40 км

4,8(42 оценок)

Открыть все ответы

Ответ:

аннаксения

27.12.2021

Найдём касательную к параболе в точке (0,5;0,75). Уравнение касательной имеет вид:
y=f'(x₀)(x-x₀)+f(x₀)
x₀=0,5
f(x₀)=0,75
f'(x)=(2x-x²)'=2-2x
f'(x₀)=2-2*0,5=2-1=1
Подставляем все найденные значения в уравнение касательной:
y=1*(x-0,5)+0,75=x-0,5+0,75=x+0,25
Площадь фигуры, ограниченной графиками функций находится по формуле:
S=∫(f(x)-g(x))dx
Верхний предел интегрирования будет равен 0,5 или 1/2 (точка касания прямой и параболы), а нижний предел интегрирования равен
x+0,25=0
x=-0,25=-1/4 (точка пересечения касательной с прямой y=0 или осью абсцисс)
Предлагаю начертить графики на координатной плоскости. Где сразу видны пределы интегрирования и график функции y=x+0,25 расположен выше графика функции y=2x-x². Записываем интеграл и решаем его:
$S= \int\limits^{ \frac{1}{2} }_{- \frac{1}{4} } {((x+0,25)-(2x-x^2))} \, dx =\int\limits^{ \frac{1}{2} }_{- \frac{1}{4} } {(x+0,25-2x+x^2)} \, dx=$
$=\int\limits^{ \frac{1}{2} }_{- \frac{1}{4} } {(x^2-x+ \frac{1}{4} )} \, dx= \frac{x^3}{3} - \frac{x^2}{2} + \frac{x}{4} |_{- \frac{1}{4} }^{ \frac{1}{2} }= \frac{1}{24}- \frac{1}{8} + \frac{1}{8}+ \frac{1}{192} + \frac{1}{32}+ \frac{1}{16}$
$= \frac{8+1+6+12}{192} = \frac{27}{192}= \frac{9}{64}$ ед²

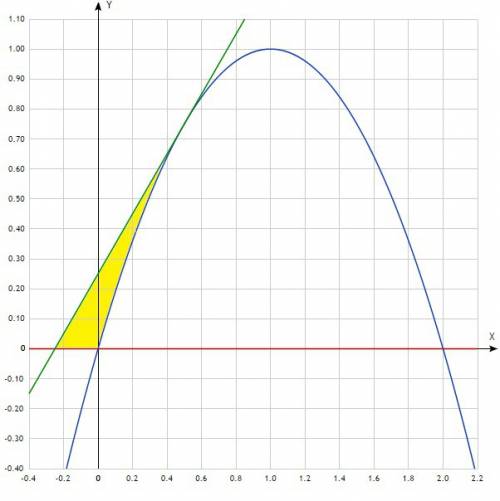
Вычислите площадь плоской фигуры,ограниченной прямой y=0,параболой y=2x-x^2 и касательной,проведенно

Вычислите площадь плоской фигуры,ограниченной прямой y=0,параболой y=2x-x^2 и касательной,проведенно

4,7(6 оценок)

Ответ:

kudgalina83

27.12.2021

Начнем с ОДЗ:

3x+6 > 0 => x > -2

2x - 4 > 0 => x > 2. Общее ОДЗ: x>3

2x - 6 > 0 => x > 3

Представим 2, как log1/2 (1/4), чтобы было удобнее считать. Далее применяем свойства суммы и разности логарифмов, и неравенство сводится к обычному дробно-рациональному. И не забываем поменять знак на противоположный, потому что основание логарифма меньше 1.

log1/2 ( (3x+6)/(2x-4) ) < log1/2 ( 1/4*(2x-6) )

log1/2 t - убывающая функция, а значит знак меняем.

(3x+6)/(2x-4) > x/2 - 6/4

(3x + 6 -x² + 2x + 3x -6) / 2(x-2) > 0

x(8 - x) / 2(x-2) > 0

Решение этого неравенства будет x ∈ ( - ∞; 0) ∪ ( 2; 8)

Из ОДЗ следует, что х>3, то ответ будет: x ∈ ( 3; 8)

ответ: (3; 8)

4,4(36 оценок)

Это интересно:

Образование-и-коммуникации

23.07.2020