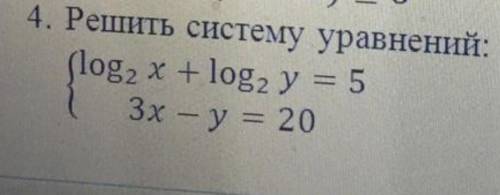
Объяснение:
Постройте график функции y=3x+2
Пользуясь графиком, найдите:
1) значение функции, если значение аргумента равно: 0; 1; -1.
2) значение аргумента, при котором значение функции равно 0.
3) несколько значений аргумента, при которых функция принимает положительные значения.
4)несколько значений аргумента, при которых функция принимает отрицательные значения.
y=3x+2
Построить график. График линейной функции, прямая линия. Придаём значения х, подставляем в уравнение, вычисляем у, записываем в таблицу. Для построения прямой достаточно двух точек, для точности построения определим три.
Таблица:
х -1 0 1
у -1 2 5
1)Согласно графика при х=0 у=2
при х= 1 у= 5
при х= -1 у= -1
2)Согласно графика у=0 при х= -2/3 (≈ -0,67)
3)Согласно графика у>0 при х∈( - 2/3; ∞), положительные значения у принимает от -2/3 до + бесконечности, например, 1, 5,10.
4)Согласно графика у<0 при х∈(- ∞; -2/3), отрицательные значения у принимает от -2/3 до - бесконечности, например, -2, -7, -25.
1) m<n, значит, в выражении m-n мы от меньшего числа отнимаем большее. В результате выйдет отрицательное число.
ответ: 1) -3,25
2) Рассмотрим третий вариант:
(2с-3)(2с+3)<4с²
4с²-9<4с²
-9<0
Утверждение справедливо для любого значения С
ответ: 3)
3) a-b<0 => a<b
c-b>0 => c>b
Мы имеем: b больше, чем а, и меньше, чем с. А меньше чем b, значит, а – наименьшее значение. С больше, чем b, значит, с – наибольшее число.
ответ: 4)
4) Если с>d, то c+1>d-3;
ответ: 2)
5) 4<а<5
Возьмём любое возможное число А (допустим, 4,5) и подставим в каждый из вариантов:
1. 7<8<9 - выражение правильное
2. 9<8<11 - выражение ложное
3. 6<8<8 - выражение ложное
4. 10<8<12 - выражение ложное
ответ: 1)
6) Формула периметра: P=2(a+b)
P=2(8,5+5,4)=27,8 – минимальное возможное значение периметра
Р=2(8,6+5,5) = 28,2 – максимальное значение периметра
Итог: 27,8<а<28,2
ответ: 3)
1)log2x+log2y=5
x–3y=–20
2)(1/3)2x–y=27
53x–y=1/25
3) x2–x–72<(или равно)0
x/3–x<0
решить уравнение
1)6sin(3x–5)=1
2)3·2x+3–2x+4=4
найдите все значения параметра а при котором эти уравнения имеют хотя бы один общий корень x2+3x+7a–21=0 x2+6x+5a–6=0