ответ: 8) n=4 или n=5
Объяснение:
дробь правильная, если числитель меньше знаменателя...
n²-n+15 < 7n+3
n²-8n+12 < 0 корни по т.Виета (2) и (6);
решение "между корнями": n ∈ (2; 6),
т.е. n∈N (по условию) может быть равно: {3; 4; 5}
остальное (сократима ли дробь) проще посчитать...
n=3: 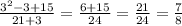 дробь сократима...
дробь сократима...
n=4: 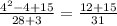 дробь НЕсократима (31-простое число))
дробь НЕсократима (31-простое число))
n=5: 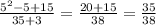 дробь НЕсократима...
дробь НЕсократима...
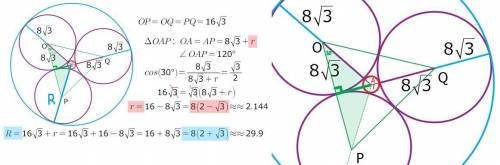
решение задачи 9) на рисунке...
таких окружностей две...
касание может быть как внутренним, так и внешним...
точки касания окружностей лежат на линии центров...
Рассмотрим случай когда уравнение не квадратное, то есть а=0:
Значит, при а=0, х=-1
Если уравнение квадратное (а≠0), то:
Дискриминант неотрицательный, значит уравнение всегда имеет 1 или 2 корня.
Если D=0, то:
При а=1/2 исходное уравнение принимает вид:
Значит, при а=1/2, х=-1
Если D>0, то:
ответ:
при
при
Рассмотрим случай когда уравнение не квадратное, то есть а=0:
Значит, при а=0, х=1
Если уравнение квадратное (а≠0), то:
Дискриминант неотрицательный, значит уравнение всегда имеет 1 или 2 корня.
Если D=0, то:
При а=1/2 уравнение имеет один корень::
Значит, при а=1/2, х=1
Если D>0, то:
ответ:
при
при