См фото, но и в объяснение загляни. это полезно
Объяснение:
Давай сначала попробуем понять, что вообще это такое
Функция - это, в первую очередь, зависимость одной переменной от другой.
Таким образом, в каждой функции есть зависимая и независимая переменная (пускай она, как и в этом случае, скрыта, но в этом случае ее видно на графике, когда он будет построен). Зависимая переменная часто обозначается буквой "у", а независимая - "х".
Перед нами - обычная линейная функция, пускай она и задана слегка непривычно.
Справка:
Линейная функция - функция, график которой - прямая линия.
Это чудо имеет особый вид записи - y=kx+b, и каждый из коэффициентов (так называются переменные k и b) указывают на что-то свое, так уж получилось. k в этой записи означает наклон графика. Если в функции положительный k - график возрастает (то есть, чем больше х, тем больше у), если отрицательный - опадает (чем меньше х, тем больше значение у).
Перед дальнейшим хочу отметить, что любая точка на координатной плоскости задается 2-мя значениями - х и у, именно в таком порядке. у - "высота" этой точки, а х - "расстояние" от точки начала координат.
С b в этом несколько проще - он означает, в какой точке график пересечет ось y, какая у этой точки будет ордината (значение y).
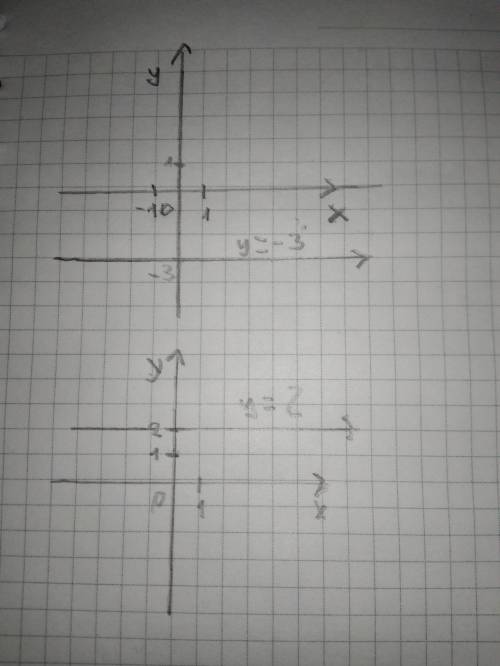
В нашем случае y=-3 х и y=2 - в функции, казалось-бы. отсутствует переменная х. Но, как бы ни так, давай попробуем все-таки построить график.
И тут мы видим, что х никуда не делся, просто наклона у функции нет. А. значит, коэффициент k стал равен 0. Таким образом, функция "в реальности" имеет вид "y=0x-3", и значение х тут не влияет на у (так как при умножении на 0 произведение всегда равно 0), и его решили убрать.
Второе - по аналогии
1. - 1;
2. 1.
Объяснение:
1. (5^2)^6•(5^7 : 5^4) /(-125)^5 = 5^(2•6) • 5^(7-4)/(-5^3)^5 = 5^12 • 5^3/(-5^15) = 5^15/(-5^15) = -1.
(✓при возведении степени в степень основание оставляем прежним, показатели умножаем;
✓при умножении степеней с одинаковыми основаниями основание оставляем прежним, показатели складываем;
✓при делении степеней с одинаковыми основаниями основание оставляем прежним, показатели вычитаем.)
2. ((-3)^9•9^2•81^3)/(-27^10 : 3^5) = ((-3)^9•9^2•81^3)/(-27^10 : 3^5) = -(3^9•(3^2)^2•(3^4)^3)/- ((3^3)^10 : 3^5) = - (3^9•(3^2)^2•(3^4)^3)/- ((3^3)^10 : 3^5) = + (3^9•3^4•3^12)/(3^30 : 3^5) = 3^25/3^25 = 1.
1. - 1;
2. 1.
Объяснение:
1. (5^2)^6•(5^7 : 5^4) /(-125)^5 = 5^(2•6) • 5^(7-4)/(-5^3)^5 = 5^12 • 5^3/(-5^15) = 5^15/(-5^15) = -1.
(✓при возведении степени в степень основание оставляем прежним, показатели умножаем;
✓при умножении степеней с одинаковыми основаниями основание оставляем прежним, показатели складываем;
✓при делении степеней с одинаковыми основаниями основание оставляем прежним, показатели вычитаем.)
2. ((-3)^9•9^2•81^3)/(-27^10 : 3^5) = ((-3)^9•9^2•81^3)/(-27^10 : 3^5) = -(3^9•(3^2)^2•(3^4)^3)/- ((3^3)^10 : 3^5) = - (3^9•(3^2)^2•(3^4)^3)/- ((3^3)^10 : 3^5) = + (3^9•3^4•3^12)/(3^30 : 3^5) = 3^25/3^25 = 1.
б у=2 это правильный ответ
Объяснение:
Б) У=2 это правильный ответ