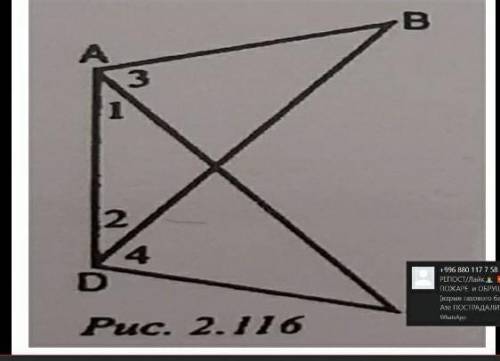
стоимость детского билета: 65 рублей
стоимость взрослого билета: 235 рублей
Объяснение:
Детский билет возьмем за неизвестную у,а взрослый билет за х,
тогда:
Ι семья 2у+х=365(руб.);
ΙΙ семья 3y+2x=665(руб.)
2у+х=365;
х=365-2у; подставим х во второе равенство 3y+2x=665,тогда:
3y+2(365-2у)=665;
3у+730-4у=665;
-у=665-730;
-у=-65;
у=65(руб.) - цена детского билета.
Найдем стоимость взрослого билета через равенство 2у+х=365:
2*65+х=365
х=235(руб.) - цена взрослого билета;
Проверка:
3y+2x=665;
3*65+2*235=665;
665=665(руб.).
ответ: 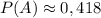 .
.
Объяснение:
В 1 урне 6 бел. и 4 чёрн. шаров, всего - 10 шаров.
Во 2 урне 4 бел. и 6 чёрн. шаров, всего - 10 шаров.
Найти вероятность события А={из 2 урны вынули белый шар } .
Гипотеза Н₁={из 1 урны вынули бел. шар} , P(H₁)=6/10 .
Переложив белый шар во 2 урну, в ней станет 11 шаров, из которых 5 белых и 6 чёрных.
Вероятность вынуть из 2 урны бел. шар равна Р(А/Н₁)=5/11 .
Гипотеза Н₂={из 1 урны вынули чёрн. шар} , Р(Н₂)=4/10 .
Переложив чёрный шар во 2 урну, в ней станет 11 шаров, из которых 4 белых и 7 чёрных.
Вероятность вынуть из 2 урны белый шар равна Р(А/Н₂)=4/11 .
По формуле полной вероятности вычисляем вероятность появления события А:
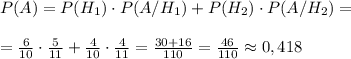
Доказательство:
Обозначим точку пересечения DB и AC буквой О. Рассмотрим треугольник aod: так как ∠1=∠2(по условию), то треугольник равнобедренный (по свойству). Теперь рассмотрим Δaob и Δdoc: ∠aob=∠doc(так как они вертикальные), также ∠3 =∠4, следовательно Δaob=Δdoc(по второму признаку равенства треугольников), а если эти треугольники равны то и сторона ab=dc.