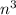 , по условию
, по условию 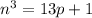 . Перенесём единицу в левую часть и разложим разность кубов на множители:
. Перенесём единицу в левую часть и разложим разность кубов на множители:
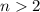 , тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение
, тогда обе скобки-сомножителя - натуральные числа, большие 1. С другой стороны, произведение 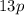 представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок
представляется в виде двух натуральных сомножителей, больших единицы, единственным (с точностью до перестановок 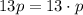 . Поэтому
. Поэтому  ,
,  равны либо
равны либо 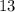 и
и 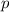 , либо
, либо 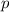 и
и 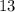 .
.
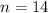 , тогда после подстановки во второе уравнение находим
, тогда после подстановки во второе уравнение находим 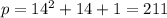 .
.  - действительно простое число, так что
- действительно простое число, так что 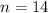 нас устраивает.
нас устраивает.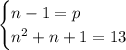
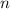 квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение
квадратное, а не линейное, как в первом случае. Упростив, получаем уравнение 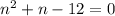 , у которого только один натуральный корень
, у которого только один натуральный корень 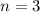 .
. - простое число, так что и тут нас всё устраивает.
- простое число, так что и тут нас всё устраивает. ,
, 
Если возвести 2 в десятую степень то есть 2¹⁰ это будет = 1024
Объяснение:2¹⁰=2*2*2*2*2*2*2*2*2*2=1024 , в степени значит умножить число на друг друга столько сколько раз написано в степени .