sin (5πx/9) = sin (πx/9) + sin (2πx/9)
sin (5πx/9) - sin (πx/9) = sin (2πx/9)
По формуле разности синусов:
2sin(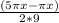
)cos(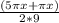
) - sin (2πx/9) = 0;
2 sin(2πx/9)cos(πx/3) - sin(2πx/9)=0;
sin (2πx/9) (2cos(πx/3)-1)=0;
sin (2πx/9)=0 или 2cos (πx/3)=1; cos (πx/3)=1/2
2πx/9=πn, n∈Z или πx/3=π/3+2πn, n∈Z или πx/3=-π/3+2πn, n∈Z;
Сокращаем на π:
2x/9=n, n∈Z или x/3=1/3+2n, n∈Z или x/3=-1/3+2n, n∈Z;
x=9n/2 или x=6n+1 или x=6n-1
Теперь отбираем корни уравнения, принадлежащие промежутку (4;8)
4<(9/2)n<8; 8/9<n<16/9; n=1, x=4,5
4<6n+1<8; 3<6n<7; 1/2<n<7/6; n=1; x=6+1=7;
4<6n-1<8; 5<6n<9; 5/6<n<3/2; n=1; x=6-1=5
ответ: x={4,5;5;7}
для начала выясним, если прибавить 11, то каждая из цифр ли увеличится на 11 или произойдет перенос разрядов. если произойдет перенос, то получится число вида Х0
для этого рассмотрим число Х0=10х=х^2-x*0+0^2=x^2, x=0, x=10
но если 10 получили прибавлением 11, то прибавляли не к двузначном числу. значит переноса не было
было число АВ=10а+b=a^2-ab+b^2
другое число CD=(A+1)(B+1)=10(a+1)+(b+1)=(a+1)^2-(a+1)(b+1)+(b+1)^2
a^2-ab+b^2+11=(a+1)^2-(a+1)(b+1)+(b+1)^2
a^2-ab+b^2+11=a^2+2a+1-ab-a-b-1+b^2+2b+1
a+b=10
выразим b=10-a и подставим:
10а+10-a=a^2-a(10-a)+(10-a)^2
9a+10=a^2-10a+a^2+100-20a+a^2
3a^2-39a+90=0
a^2-13a+30=0
(a-10)(a-3)=0
a=10 - между прочим, не цифра
а=3, b=10-3=7
число 37
после увеличения на 11 это 48
ответ: 37 и 48
65
Объяснение:
Если одна площадь больше другой на 1, а другая больше третьей на 64, то первая больше третьей на 1+64=65. Этот же ответ можно получить и по другому. Если решать систему из трех уравнений если сложить все прямоугольники то получится a+b+a+c+b+c=130
2a+2b+2c=130
2(a+b+c)=130
a+b+c=65