
2)

2x ≠ -1 ⇒ x ≠ -0.5
x -5 = 0 ⇒ x = 5
Метод интервалов
+ - +
(- 0,5) [5]
x ∈ (-0.5; 5]
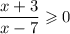
х ≠ 7
х + 3 = 0 ⇒ х = -3
Метод интервалов
+ - +
[- 3] (7)
x ∈ (-∞; -3]∪ (7; +∞)
4)
-x² - 5x + 6 ≤ 0
-x² - 5x + 6 = 0
D = 25 +24 = 49 = 7²
x₁ = -0.5 · (5 - 7) = 1
x₂ = -0.5 · (5 + 7) = -6
Метод интервалов
- + -
[- 6] [1]
x ∈ (-∞; -6] ∪ [1; + ∞)
3x² - 8x - 3 ≥ 0
3x² - 8x - 3 = 0
D = 64 +36 = 100 = 10²
x₁ = (8 - 10) : 6 = -1/3
x₂ = (8 + 10) : 6 = 3
Метод интервалов
+ - +
[- 1/3] [3]
x ∈ (-∞; -1/3] ∪ [3; + ∞)
Получим
(x - 1)*(x + 3)^2 - 5*(x + 3) = 0
Выносим общий множитель, имеем
( x + 3)*( (x - 1)*( x + 3) - 5) = 0
Аккуратно раскрываем скобки, приводим подобные
( x + 3)*( x^2 + 3x - x - 3 - 5) = 0
( x + 3 )*( x^2 + 2x - 8) = 0
Приравниваем каждое к нулю и решаем отдельно
(1)
x + 3 = 0
x₁ = - 3
(2)
x^2 + 2x - 8 = 0
Решим квадратное уравнение через дискриминант
D = b^2 + 4ac = 4 + 4*8 = 36 = 6^2 > 0
x₂ = ( - 2 + 6)/2 = 4/2 = 2;
x₃ = ( - 2 - 6)/2 = - 8/2 = - 4;
ответ :
- 4; - 3; 2