1)6у²-9у+4у-6=6у²-5у-6
2)-10ab+5а²+2b²-ab=-11ab+5а²+2b²
3)24х³+28х²+6х²+7х=24х³+34х²+7х
4)18а³-18а²+45а+2а²-2а+5=18а³-16а²+43а+5
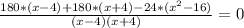
1) подкоренное выражение четной степени -должно быть положительно ( в примере корень второй степени)
x^2-6x+8≥0
D=36-32=4
x1=(6+2)/2=4
x2=(6-2)/2=2
так как парабола ветвями вверх (коэффициент пере x^2 положителен)
то методом интервалов
[2][4]
ответ: x=(-∞;2]U[4;+∞)
2)знаменатель дроби не равен 0, поэтому x-1≠0; x≠1
показатель логарифма положителен
(4-x^2)/(x-1)>0
корни когда левая часть обращается в 0 x=-2;2;1-их выкидываем и определяем знак в промежутках между ними
(-2)---(1)(2)
ответ x=(-∞;-2)U(1;2)
3)знаменатель не равен 0, поэтому log21(x+3)≠0; x+3≠21^0
x+3≠1; x≠-2
показатель логарифма положителен, поэтому x+3>0; x>-3
подкоренное выражение ≥0
25-x^2≥0; x^2≤25; x=[-5;5]
учитывая все три условия-получаю
ответ x=(-3;-2)U(-2;5]
(3y+2)(2y-3) = 6y² - 5y -6
(-5a+b)(2b-a) = -11ab + 5a² + 2b²
(4x²+x)(6x+7) = 24x³ + 34x² + 7x
(9a+1)(2a²-2a+5) = 18a³ - 16a² + 43a + 5