y=x²-2x+3
А) хо= -b/2a = -(-2)/2 = 2/2 =1
yo= f(xo) = 1²-2*1+3 = 1-2+3= 2
(1; 2)
Б) Ось симиетрии параболы -- это, по сути, просто приравнивание игрека к хо: у=1
В) С осью Ох:
На оси Ох ордината равна нулю, поэтому просто заменяем игрек на ноль и решаем
x²-2x+3=0
D= (-2)²-4*3 = 4-12= -8
D<0
График не имеет точки пересечения с осью Ох ∅.
С осью Оу:
На оси ординат значение абсциссы (х) равно нулю. Поэтому подставляем вместо икса ноль:
y=0²-2*0+3
y=3
Поэтому точка пересечения данного графика с осью Оу -- (0; 3)
Г) на фото. Направление веток параболы--вверх, потому что а>0
Еще мы там уточняем график
Д) в первой и во второй
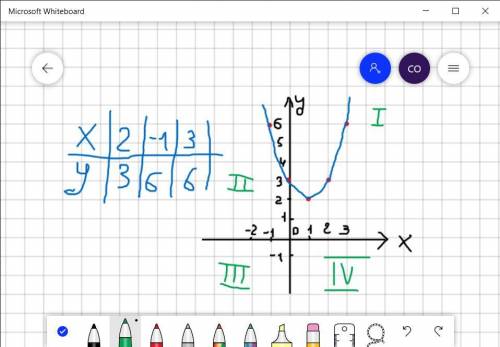
х³(2х+3)-4х(2х+3)=0
(2х+3)(х³-4х)=0
х(х²-4)(2х+3)=0
х(х-2)(х+2)(2х+3)=0
х=0 х-2=0 х+2=0 2х+3=0
х=2 х=-2 2х=-3
х=-1,5
ответ: -2; -1,5; 0; 2
2) 5х³+3х²-5х-3=0
х²(5х+3)-(5х+3)=0
(5х+3)(х²-1)=0
(5х+3)(х-1)(х+1)=0
5х+3=0 х-1=0 х+1=0
5х=-3 х=1 х=-1
х=-0,6
ответ: -1; -0,6; 1.
3) х⁴+2х³+2х²+2х+1=0
(х⁴+2х²+1)+(2х³+2х)=0
(х²+1)²+2х(х²+1)=0
(х²+1)(х²+1+2х)=0
(х²+1)(х²+2х+1)=0
(х²+1)(х+1)²=0
х²+1=0 (х+1)²=0
х²=-1 х+1=0
нет решений х=-1
ответ: -1.