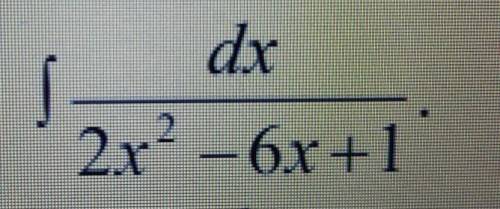
докажем утверждение от противного.
можно предположить, что для любых двух разных точек a и b из s найдется отличная от них точка x из s такая, что либо xa < 0,999ab, либо xb < 0,999ab.
переформулируем утверждение: для любого отрезка i с концами в s и длиной l найдется отрезок i′ с концами в s длины не более 0,999l, один из концов которого совпадает с некоторым концом i.
или, иначе говоря, i′ пересекает i.
возьмем теперь первый отрезок i1 длины l и будем брать отрезки i2, i3, …так, что ik + 1 пересекается с ik и |ik + 1| < 0,999|ik|.
все эти отрезки имеют концы в s. ломаная не короче отрезка, соединяющего ее концы, поэтому расстояние от любого конца ik до любого конца i1 не превосходит
следовательно, в квадрате 2000l × 2000l с центром в любом из концов i1 лежит бесконечное число точек s.
но из условия следует конечность их числа в любом квадрате.
√(a-b) / b
Объяснение:
Вторую скобку переводим в дробь:
1 + √((a+b)/(a-b)) = 1 + √(a+b)/√(a-b) = [√(a-b) + √(a+b)] / √(a-b)
Дальше, мы делим на эту дробь, то есть умножаем на перевёрнутую.
[2√a + √(a+b) - √(a-b)]*√(a-b)
(√a - √(a-b))*(√a + √(a+b))*(√(a-b) + √(a+b))
И тут самое главное: оставить числитель и разложить знаменатель:
[a - √a√(a-b) + √a√(a+b) - √(a-b)√(a+b)]*(√(a-b) + √(a+b)) =
= a√(a-b) - (a-b)√a + √a√(a^2-b^2) - (a-b)√(a+b) +
+ a√(a+b) - √a√(a^2-b^2) + (a+b)√a - (a+b)√(a-b) =
= a√(a-b) - a√a + b√a - a√(a+b) + b√(a+b) + a√(a+b) + a√a + b√a - a√(a-b) - b√(a-b) =
= 2b√a + b√(a+b) - b√(a-b) = b*(2√a + √(a+b) - √(a-b)
Получаем такую дробь:
(2√a + √(a+b) - √(a-b))*√(a-b)
b*(2√a + √(a+b) - √(a-b))
Две большие скобки сокращаются, и остаётся:
√(a-b) / b
Выделяем квадрат в знаменателе: