От остановки электрички в перпендикулярных направлениях одновременно двинулись велосипедист игорь со скоростью 12км/ч и пешеход дима со скоростью 5км/ч. через какое время расстояние между игорем и димой будет равно 26км? нужно составить квадратное уравнение. нужно.
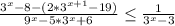
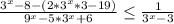
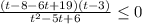
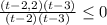
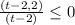
5x-расстояние пешехода
По теореме Пифагора
144х^2+25х^2=676
169х^2=676
х^2=4
х1=2 х2=-2(не удовлетворяет условия задачи)
ответ:Через 2 часа.