Відповідь
Пояснення:
(72-9*0.01)*(72+90.01)-49*2*2
(72-0.09)*162.01-196
71.91*162.01-196
11650.1391-196
11454.1391
См. рисунок в приложении.
а) На отрезке [π/6; 2·π/3] функция y=cosx убывает, поэтому:
наибольшего значения достигает в левой границе, то есть при x = π/6: y(π/6)=√3/2;наименьшего значения достигает в правой границе, то есть при x = 2·π/3: y(2·π/3) = -1/2б) интервал (-π; π/4) содержит значения x=-π и x = 0, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = -π: y(-π) = -1;в) луч [-π/3; +∞) содержит значения x=0 и x = π, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = π: y(π) = -1;г) полуинтервал [-π/3; 3π/2) содержит значения x=0 и x = π, в которых функция y=cosx:
достигает наибольшего значения при x = 0: y(0) = 1;достигает наименьшего значения при x = π: y(π) = -1.![Найдите наименьшее и наибольшее значение функции y=cosx а) на отрезке [π/6; 2π/3] б) на интервале (-](/tpl/images/0936/5711/c9260.jpg)
Общий вид квадратного уравнение следующее
a·x²+b·x+c=0, где a≠0.
Неполное квадратное уравнение имеет один из следующих видов:
a·x²+c=0 когда b=0; a·x²+b·x=0 когда c=0;a·x² = 0 когда b=c=0.1. a) Если неполное квадратное уравнение имеет вид a·x²+c=0 и c/a<0, то квадратное уравнение a·x²+c=0 имеет корни равные по модулю, но противоположные по знаку:
a·x²+c=0 ⇔ a·x² = -c ⇔ x² = -c/a, так как -c/a>0 ⇔ 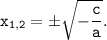
Тогда
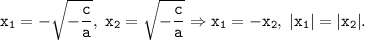
Отсюда условие:
b=0 и c/a<0!
b) Если неполное квадратное уравнение имеет вид a·x²=0, то квадратное уравнение a·x²=0 имеет единственный корень:
a·x²=0 ⇔ x²=0 ⇔ x=0.
Отсюда условие:
b=c=0!
В случае a·x²+b·x=0 квадратное уравнение имеет два корня:
a·x²+b·x=0 ⇔ x·(a·x+b)=0 ⇒ x₁=0, x₂= -b/a.
79-9y*72+90,01-49x2=169,01-648y-98x
если x=2, y=0,01, то 169,01-648*0,01-98*2=-33,47
ответ:-33,47