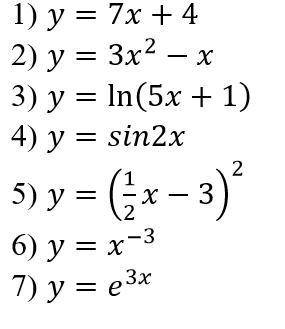
x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
Объяснение:
x1 = -re(acos(-3)) + 2*pi - i*im(acos(-3))
x2 = 2*pi - i*im(acos(4))
x3 = re(acos(-3)) + i*im(acos(-3))
x4 = re(acos(4)) + i*im(acos(4))
x1 = 3.14159265358979 + 1.76274717403909*i
x2 = 6.28318530717959 - 2.06343706889556*i
x3 = 3.14159265358979 - 1.76274717403909*i
x4 = 2.06343706889556*i
сумма
-re(acos(-3)) + 2*pi - i*im(acos(-3)) + 2*pi - i*im(acos(4)) + i*im(acos(-3)) + re(acos(-3)) + i*im(acos(4)) + re(acos(4))
=
4*pi + re(acos(4))
произведение
(((-re(acos(-3)) + 2*pi - i*im(acos(-3)))*(2*pi - i*im(acos(4*(i*im(acos(-3)) + re(acos(-3*(i*im(acos(4)) + re(acos(4)))
=
-(2*pi - i*im(acos(4)))*(i*im(acos(-3)) + re(acos(-3)))*(i*im(acos(4)) + re(acos(4)))*(-2*pi + i*im(acos(-3)) + re(acos(-3)))
Для того, чтобы найти сумму первых двадцати членов арифметической прогрессии заданной формулой n - го члена прогрессии an = 3n + 2 прежде всего вспомним формулу для нахождения суммы n первых членов арифметической прогрессии.
Sn= (a1 + an)/2 * n.
Из заданной формулы найдем первый и двадцатый член арифметической прогрессии:
a1 = 3 * 1 + 2 = 3 + 2 = 5;
a20 = 3 * 20 + 2 = 60 + 2 = 62.
Теперь можем подставить найденные значения в формулу для нахождения суммы и произвести вычисления.
S20= (a1 + a20)/2 * 20 = (5 + 62)/2 * 20 = 67/2 * 20 = 67 * 10= 670.
Объяснение:
Производные
Объяснение:
1) y=7x+4 y'=7 y'(0)=7
2) y=3^2(X) - x y'=6x - 1 y'(0)=6*0 -1= -1
3) y=ln(5x+1)=5/5x+1 y'(0)=5/5*0+1=5
4) y=sin2x y'= 2cos(2x) y'(0)=2*cos(2*0)=2*1=2
5) y=(0,5x -3)^2=(0,5x-3)(0,5x-3) y'=0,5*(0,5x-3) + (0,5x+3)*0,5= 0,5x -3
y'(0)=0.5*0-3= -3
6) y=x^-3= 1/x^3 y'= -3/x^4 y'(0)=-3/0^4=0
7) y=e^3x y'=3*e^3x y'(0)=3*e^3*0= 3*1=3