ответ: 4132 .
Угловой коэффициент прямой k - это тангенс угла наклона ( tgα ) прямой к положительному направлению оси ОХ.
Все острые углы α имеют положительный tgα>0 , а тупые углы - отрицательный tgα<0 .
Прямые 1 и 4 наклонены под острым углом, значит их угловые коэффициенты положительны ( k₁>0 , k₄>0 ) . А прямые 2 и 3 наклонены под тупым углом к оси ОХ , значит их угловые коэффициенты отрицательны ( k₂<0 , k₃<0 ) .
Все положительные числа больше отрицательных . Теперь сравним между собой k₁ и k₄ , а также k₂ и k₃ .
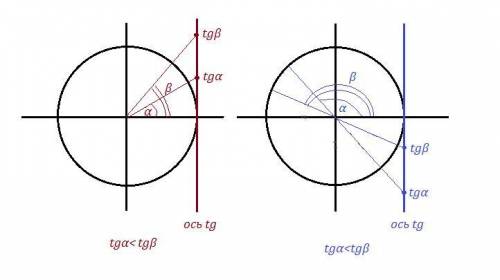
Чем больше острый угол, тем больше tg этого угла , значит k₄>k₁ .
Чем меньше тупой угол, тем меньше tg этого угла, значит k₃>k₂ .
Окончательно получаем: k₄>k₁>k₃>k₂ .
1) f(x)=7x-14, [0;4]
производная равна 7, 7≠0, , поэтому нет критических точек, и наибольшее и наименьшее свое значение функция принимает на концах отрезка.
f(0) = -14-наименьшее значение.
f(4) =14 наибольшее значение функции
2) f(x)= -0,2x + 0,4, [1;3]
аналогично 1) производная -0.2≠0, ищем значения функции на концах отрезка, т.е. f(1) =-0.2+0.4=0.2- наибольшее значение.
f(3) =-0.6+0.4=-0.2-наименьшее значение.
3) f(x)= 6/x, [1;6]
производная равна -6/х²≠0, не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(1) =6/1=6- наибольшее значение.
f(6) =6/6=1- наименьшее значение.
4) f(x)= -5/x, [-5;-1]
Производная равна 5/х²≠0 не существует в точке 0, но эта точка не входит и в область определения. ищем значения функции на концах отрезка, т.е. f(-1) =-5/(-1)=5- наибольшее значение.
f(-5) =-5/(-5)=1- наименьшее значение.