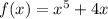
Найдем производную:
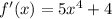
Выражение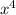 
принимает только неотрицательные значения. Значит, выражение 
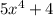принимает только положительные значения.
Таким образом, производная функции на всей области определения положительна. На промежутках, где производная положительна, функция возрастает. Значит, функция возрастает на всей области определения R.
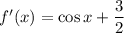
Найдем область значений производной:
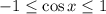
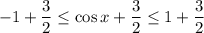
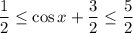
Производная принимает только положительные значения на всей области определения. На промежутках, где производная положительна, функция возрастает. Соответственно, функция возрастает на всей области определения R.
Объяснение:
Найти площадь фигуры, ограниченной линиями:
у=х² +6х+12; х=-1; х=-3; у = 0
Построим указанные кривые на координатной плоскости
у=х² +6х+12 - уравнение параболы. Однозначно строится по трем точкам. Вершина параболы находится в точке с координатами(-3;3).
Еще две точки найдем подставив координаты х = -1 и х = -3 в уравнение параболы
у(-3) = 9 - 18 + 12 = 3
у(-1) = 1 - 6 + 12 = 7
Координаты двух других точек (-3;3) и (-1;7)
Уравнения х=-1; х=-3 на координатной плоскости описывают прямые.
Данные прямые параллельны оси абсцисс и проходят через точки (-1;0) и (-3;0) соответственно.
Прямая y=0 является осью ординат.
Фигура внутри полученного пересечения снизу ограничена прямой y=0 справа ограничена прямой х = -1, слева прямой х=-3, а сверху ограничена параболой у=х² +6х+12
Для нахождения площади фигуры найдем интеграл с пределами интегрирования от -3 до -1 и функцией х² +6х+12