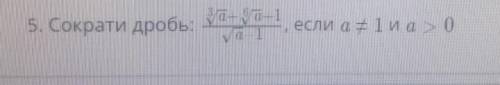
1) 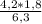 =
= 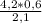 =
= 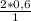 = 1,2
= 1,2
2) Так как a лежит равноудаленно от двух противоположных по знаку чисел, то a = 0. Следовательно, правильный ответ - 3
3)
4,5 = √(20,25)2√6 = √(4*6) = √242√5 = √(4*5) = √20√22Наименьшее - √20. ответ - 3
4) 2 + 3*(х-3) = 2х - 6
2 + 3x - 9 = 2x - 6
3x - 2x = -6 + (-2) + 9
x = 1
5) А - 3; Б - 2; В - 1
6) aₙ = 4n - 4 ⇒ 4n = aₙ + 4 ⇒ n = 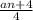
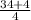 = 9,5 - не может быть, т.к. порядковый номер должен быть целым числом
= 9,5 - не может быть, т.к. порядковый номер должен быть целым числом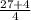 = 7,75 - неверно
= 7,75 - неверно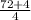 = 19 - верно
= 19 - верно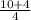 = 3,5 - неверное
= 3,5 - неверноеответ - 3
7) 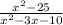 =
= 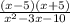
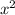 - 3x - 10 = 0
- 3x - 10 = 0
По теореме Фиета корни - +5 и -2 ⇒ 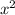 - 3x - 10 ⇔ (x-5)(x+2)
- 3x - 10 ⇔ (x-5)(x+2)
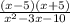 =
= 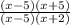 =
= 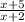
8) -2x² - 5x ≥ -3 2x² + 5x - 3 = 0
-2x² - 5x + 3 ≥ 0 | ×(-1) D = 25 + 24 = 49 = 7²
2x² + 5x - 3 ≤ 0 x₁ = 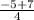 = 0,5; x₂ =
= 0,5; x₂ = 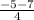 = -3
= -3
(x - 0,5)(x + 3) ≤ 0
На промежутке ( -∞; -3] - x ≥ 0
На промежутке [ -3; 0,5] - x ≤ 0
На промежутке [0,5; +∞) - x ≥ 0
ответ: x ∈ [ -3; 0,5]
9)
1) В ΔABL ∠ABL = ∠BAL = 23° (равные углы при основании равнобедренного Δ-ка);
2) ∠BAL = 2∠A ⇒ ∠A = 46°;
3) ∠C = 180° - ∠A - ∠B = 180° - 46° - 23° = 111°
ответ: 111
10)
1) В ΔAHC cos∠A = 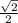 ⇒ ∠A = 45°
⇒ ∠A = 45°
2) sin∠45° = 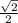 ⇒
⇒ 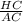 =
= 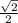 ⇒ AC =
⇒ AC = 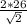 =
= 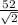
3) По т. Пифагора AC² = (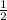 AB)² + CH² ⇒ (
AB)² + CH² ⇒ (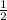 AB)² =
AB)² = 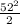 - 26² = 26 * 52 - 26 * 26 = 26 * (52 - 26) = 26²
- 26² = 26 * 52 - 26 * 26 = 26 * (52 - 26) = 26²
4) (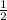 AB)² = 26² ⇒
AB)² = 26² ⇒ 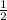 AB = 26 ⇒ AB = 52
AB = 26 ⇒ AB = 52
ответ: 52
11)
1) S = 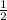 * AB * AC * sin∠A (площадь треугольника равна половине произведения сторон на синус угла между ними)
* AB * AC * sin∠A (площадь треугольника равна половине произведения сторон на синус угла между ними)
2) sin²∠A = 1 - cos²∠A ⇒ sin²∠A = 1 - (-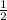 )² = 1 -
)² = 1 - 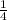 =
= 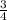 ⇒ sin∠A =
⇒ sin∠A = 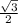
3) S = 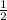 * 4 * 4 *
* 4 * 4 * 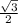 = 4
= 4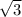
ответ: 4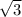
12)
tg∠ABC = 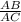 =
=  = 1
= 1
tg∠45° = 1 ⇒ ∠ABC = 45°
ответ: 45°
13)
1 - неверно
2 - неверно
3 - верно
ответ: 3
14)
Оценка "5" за время, меньшее 17,5 сек
Оценка "4" за время от 17,5 до 18,5
За 18 секунд - оценка "4"
ответ: 4
15)
ответ: 10
16)
15.000 * (1 - 0,18) = 15.000 * 0,82 = 12300
ответ: 12300
17)
Найдем тангенс угла, под которым от человека падает тень:
tg = 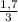
Этому же значению будет равно отношение высоты фонаря к расстоянию от фонаря до тени. Возьмем высоту фонаря как x, получаем уравнение: 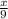 =
= 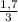 ⇒ х =
⇒ х = 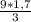 = 3 * 1,7 = 5,1м
= 3 * 1,7 = 5,1м
ответ: 5,1
18)
ответ: 2
19)
Мальчиков - 2, девочек - 3, всего - 5
Шанс того, что мальчики начнут игру = 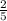 = 0,4
= 0,4
ответ: 0,4
20)
S падения = 3 * 4 + 5 * 4²
S = 92 м (за 4 секунды камень пролетел 92 метра)
h = 150 - 92 = 58
ответ: 58
Объяснение:
1. В примере а) коэффициенты k= равны 0,5, значит их графики параллельны.
В примере в) коэффициенты k=5, значит их графики параллельны.
2. ответ 3. Кубическая парабола, ветви графика расположены в 1 и 3 четвертях.
3. АБВГ
2413
4. 2x + y = 8
2x - y = 1
Из первого уравнения y = 8 - 2x. Тогда подставляем выражение во второе уравнение:
2x - (8 - 2x) = 1
2x - 8 + 2x = 1
4x = 9
x = 2,25
y = 8 - 2*2,25 = 8 - 4,5 = 3,5
ответ: (2,25; 3,5)
5. а) 1) y = 3x+1. Область определения функции - все действительные значения аргумента.
2) 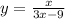 . Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
. Область определения: 3x - 9 не равно нулю. Значит, x не равен 3. Следовательно, все, кроме 3.
б)  при
при 
Если x = -5, то 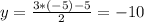
Если х= 3, то 
Значит, 
Объяснение: