S = 4
Объяснение:
Найдём уравнение прямой, проходящей через точки (-3; 0) и (-1; 3).
(х + 3)/(-1 + 3) = (у -0)/(3 - 0)
3(х + 3) = 2у
у = 1,5х + 4,5
Найдём точки пересечения этой прямой с осью Ох
у = 0;
1,5х + 4,5 = 0
х = -3
парабола у = 3х касается оси Ох в точке х = 0.
Найдём точки пересечения параболы у = 3х² и прямой у = 1,5х + 4,5
3х² = 1,5х + 4,5
3х² - 1,5х - 4,5 = 0
2х² - х - 3 = 0
D = 1 + 24 = 25
x1 = (1 - 5)/4 = -1
x2 = (1 + 5)/4 = 1.5
Изобразим графики, заданные уравнениями параболы и прямой.
Смотри рисунок на прикреплённом файле.
Очевидно, что фигура, заключённая между параболой, наклонной прямой и осью Ох, представляет собой криволинейный треугольник. Причем левая половина этого треугольника ограничена наклонной прямой и осью Ох, а правая половина - параболой и осью Ох. Соответственно, и интегралов будет два
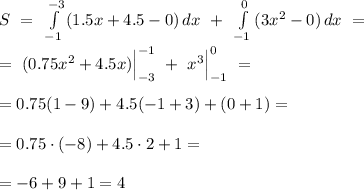
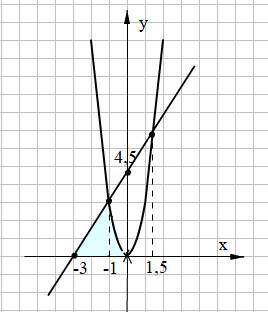
y^24
Объяснение:
сначала степень 2 умножаешь на 3, получается 6, затем 6 умножаешь на степень 4, получается 24.