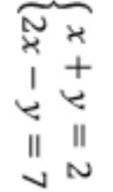
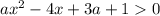
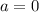квадратное неравенство вырождается в линейное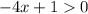
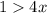
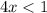
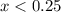
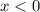
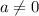
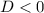) - отлично, график параболы выше оси Ох - неравенство выполняется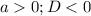
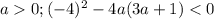
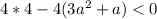
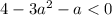
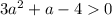
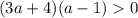
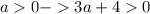авмтоматически
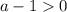или 
- 
; 
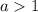
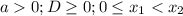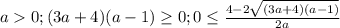
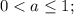- с первых двух неравенств (аналогично по рассуждениям относительно первого случая)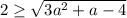
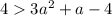
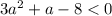- что очевидно верно при условиях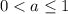 
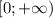
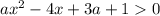
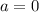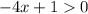
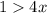
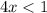
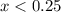
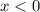
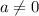
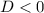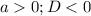
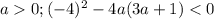
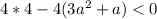
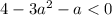
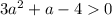
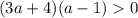
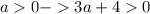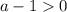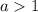
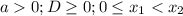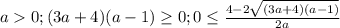
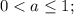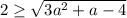
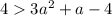
квадратное неравенство вырождается в линейное) - отлично, график параболы выше оси Ох - неравенство выполняется авмтоматически или - ; - с первых двух неравенств (аналогично по рассуждениям относительно первого случая) 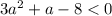- что очевидно верно при условиях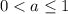
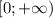
ответ: (3;-1)
Сначала приведём уравнение к обычному виду
у= - х+2
у=2х-7
Первый график - синий
второй график - красный
решение- координаты точки пересечения х=3 у=-1