Подобные одночлены - это одночлены, которые состоят из одних и тех же букв, в одинаковых степенях, но с разными или одинаковыми коэффициентами (числовыми множителями).
В этих выражениях требуется представить одинаковые множители как степень одного множителя.
1. -3,1*babab = -3,1*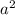
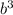, подобным ему будет 2/5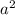
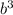
2. 2 1/3*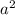ba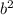
*(-3) = -7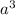
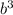, подобным ему будет -3,1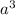
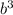
3. 1/5bab*2 = 2/5a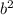, подобным ему будет -7a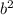
Похоже это задание на внимательность, чтобы правильно понимать смысл подобных одночленов и не вестись на одинаковые коэффициенты.
Объяснение:
1) Kl=12; KM:ML= 3 : 1
KM=3ML
KM+ML=KL
3ML+ML=12
4ML=12
ML=3
KM=3ML=9
2) AB/ED=YX/LK; AB= 2 см, ED= 3 см и LK= 27 см
YX=LK·AB/ED=27·2/3=54/3=18
YX=18 см
3) ΔKBC∼ΔRTG; k= 18; P₁=8; S₁=9; P₂=?, S₂=?
Условие не полное. Не определена зависимость сторон от коэффициента подобия к. То есть какие стороны подобны(это не обязательно), а главное порядок отношения сторон относительно к.
Рассмотрю оба случая:
a) ΔKBC∼ΔRTG⇒P₂/P₁=k; S₂/S₁=k²
P₂=kP₁=8·18=144 см
S₂=k²S₁=8²·9=64·9=576 см²
б) ΔKBC∼ΔRTG⇒P₁/P₂=k; S₁/S₂=k²
P₂=P₁/=18/8=2,25 см
S₂=S₁/k²=9/8²=9/64 см²
Прямая пропорциональности задается формулой " Y= k*x
график проходит через точку , значит 4=к*(-1)
k=-4
Прямая пропрциональность задается формулой у=(-4)x