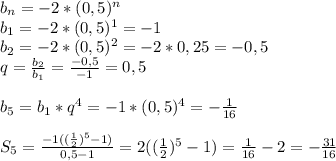
1. коэффициент а
a=0 это функция становится линейной y=bx+c
a>0 ветви параболы направлены вверх
a<0 ветви параболы направлены вниз
2. коэффициент с
это точка пересечения графика с осью OY (при x=0)
c>0 пересечение выше оси OX (y>0)
c<0 пересечение ниже оси ОХ (y<0)
c=0 пересечение проходит через начало координат
3. коэффициент b
вершина параболы (абсцисса) вычисляется x(верш) = -b/2a
b = -2a*x(верш)
b = 0 вершина параболы лежит на оси OY
x(верш)>0 вершина расположена правее оси OY
x(верш)<0 вершина левее оси ОY
для того чтобы точно определить по графику знак b надо смотреть на знак a
кроме того b - коэффициент, который отвечает за симметрию.
При b=0 симметрия полная относительно оси OY.
4. очень многое зависит и от дискриминанта D=b²-4ac
если D=0 то график функции касается оси ОХ
если D<0 то график не касается оси ОХ
если D>0 то графие пересекает ось ОХ в двух точках
bn=-2(0.5)^n
b1= -2(0.5)¹ = -1
b2 = -2(0.5)² = -0.5
q= -0.5 / (-1) = 0.5
b5=-2(0.5)⁵ = -1/16 = -0.0625
S5 = (b5*q-b1) / (q-1) = (-0.0625*0.5+1) / (0.5-1) = (-0.03125+1) / (-0.5) = 0.96875/(-0.5) = -1.9375
ответ: S5 = -1.9375
расчитаем тоже самое в обыкновенных дробях:
S5 = (b5*q-b1) / (q-1)
b5*q-b1 = (-1/16 * (1/2) +1) = -1/32 +1 = 31/32
q-1 = 1/2 - 1 = -1/2
S5= 31/32 : (-1/2) = -(31*2)/32 = -31/16
ответ: S5= -31/16