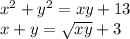
Объяснение:
Уравнение касательной имеет вид:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
Дана функция:
f(x)=-x^2-4x+2f(x)=−x
2
−4x+2
Найдём значение функции в точке x₀:
f(x_0)=f(-1)=-(-1)^2-4 \cdot (-1)+2=-1+4+2=5f(x
0
)=f(−1)=−(−1)
2
−4⋅(−1)+2=−1+4+2=5
Найдём производную функции:
f'(x)=-2x^{2-1}-4=-2x-4f
′
(x)=−2x
2−1
−4=−2x−4
Найдём производную функции в точке x₀:
f'(x_0)=f'(-1)=-2 \cdot (-1) -4 =2-4=-2f
′
(x
0
)=f
′
(−1)=−2⋅(−1)−4=2−4=−2
Подставим найденные значения, чтобы найти уравнение касательной:
y=f(x_0)+f'(x_0)(x-x_0)y=f(x
0
)+f
′
(x
0
)(x−x
0
)
y=5+(-2)(x-(-1))y=5+(−2)(x−(−1))
y=5-2(x+1)y=5−2(x+1)
y=5-2x-2y=5−2x−2
\boxed{y=-2x+3}
y=−2x+3
ответ: y=-2x+3 - искомое уравнение.
1) a) 4+12x+9x2
4+12x+18
22+12x
2(11+6x)
б) 25-40х+16х2
25-40х+32
57-40х
г) -56а+49а*2+16
-56а+98а+16
42а+16
2(21а+8)
2) a) (y-1)(y+1) б) p^2-9 г) (3x-2)(3x+2) д) (3x)^2-2^2 е) a^2-3^2
y^2-1 (3x)^2-2^2 9x^2-4 a^2-9
в) 4^2-(5y^2) 9x^2-4
16-25y^2
4) a) a3-b3 б) 27a3+8b3
3(a-b) 81a+24b
3(27a+8b)
x² + y² = xy + 13
x + y = √xy + 3
x, y одного знака > 0
(x + y)² = x² + y² + 2xy
x² + y² = (x + y)² - 2xy
замена
√xy = t > 0
x + y = u
Система
u² = 3t² + 13
u = t + 3
t² + 6t + 9 = 3t² + 13
2t² - 6t + 4 = 0
t² - 3t + 2 = 0
D = 9 - 8 = 1
t12 = (3 +- 1)/2 = 1 2
1. t = 1
u = 4
√xy = 1
x + y = 4
x = 4 - y
y(4 - y) = 1
y² - 4y + 1 = 0
D = 16 - 4 = 12
y12 = (4 +- √12)/2 = 2 +- √3
y1 = 2 + √3
x1 = 4 - y1 = 2 - √3
y2 = 2 - √3
x2 = 2 + √3
2. t = 2
u = 5
√xy = 2
x + y = 5
x = 5 - y
y(5 - y) = 4
y² - 5y + 4 = 0
D = (25 - 16) = 9
y34 = (5 +- 3)/2 = 1 4
y3 = 1
x3 = 5 - y3 = 4
y4 = 4
x4 = 1
ответ (1, 4) (4, 1) (2 - √3, 2 + √3) (2 + √3, 2 - √3)