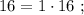
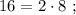
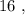т.е.: 
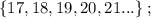
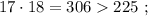
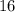каждое – будет, очевидно, больше чем 
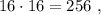т.е. больше 
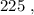а значит, при выборе минимальных чисел в виде 
и 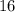– подобрать остальные числа невозможно.
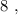т.е.: 
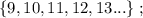
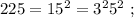
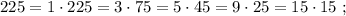
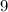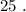
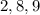и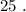 
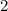и 
и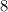 
Вася никаких чисел добавить не мог бы, поскольку тогда минимальные числа стали бы другими, и их произведение уже не было бы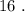 
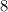и 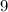никаких натуральных чисел нет. 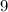и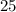 
Вася тоже никаких чисел добавить не мог бы, поскольку тогда максимальные числа стали бы другими, и их произведение уже не было бы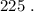 
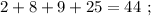
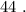
Рассшифруем условие задачи
Итак, участок АС:
Это расстояние мотоциклист проехал за время t час, со скоростью 90 км/час
тогда автомобиль проехал это расстояние за t+1 час со скоростью х км/час
Так как они встретились в точке С то их пути равны: получили первое уравнение
90*t=(t+1)*х
Далее мотоциклист поехал обратно ( и как не странно АС=СА) значит времени затратил тоже t час. И за это время автомобиль доехал до B
Значит на весь путь автомобиль потратил t+1+t=2t+1 час и двигался со скоростью х км/час и проехал путь 300км
Получили второе уравнение
x*(2t+1)=300
решим нашу систему
из первого уравнение выразим х
подставим во второе
Значит время на путь от АС 2 часа
Расстояние 90*2=180 км