Раскрой скобки: (x−11)⋅(x+1)

Question

Алгебра: Раскрой скобки: (x−11)⋅(x+1)

dimapivovarov · Accepted Answer

Давайте для начала формализуем условие. У насть есть вероятностное простравнство Ω. Что такое в нём исход? Исход - это как раз передача сообщения n раз. Исход можно закодировать последовательностью n+1 чисел. Каждое число в последовательности обозначает жителя, а следующее жителя которому будет передано сообщение. Получаем, что:

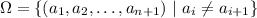
$\Omega = \{ (a_1,a_2,\ldots,a_{n+1}) \,\, | \, \, a_i \neq a_{i+1} \}$

Из условия следует, что каждый исход равновероятен. 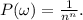$P(\omega) = \frac{1}{n^n}.$

Теперь посчитаем вероятность, что новость будет передана n раз без повторного сообщения её кому-нибудь. Обозначим это событие как A. Заметим, что каждый благоприятный исход (лежит в А) представляет собой перестановку (n+1)-го чисел. Всего таких перестановок 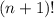(n+1)! . Теперь можно считать вероятность:

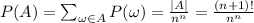
$P(A) = \sum_{\omega \in A} P(\omega) = \frac{|A|}{n^n} = \frac{(n+1)!}{n^n}$

MOGZ ответил